AB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
The correct Answer is:1
Step by step video, text & image solution for AB is a diameter of a circle and AC is its chord such that angleBAC=30^(@). If the tengent at C intersects AB extended at D, then BC=BD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - OBJECTIVE Type Questions (Very Short Questions)
10 Videos
- CIRCLESBOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - SHORT ANSWER (SA-I) Type Questions
28 Videos
- CIRCLESBOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - OBJECTIVE Type Questions (Fill in the Blanks)
9 Videos
- CBSE TERM-1 SAMPLE PAPER 2BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM-1 SAMPLE PAPER 2EXERCISE - Section -C
7 Videos
- CONSTRUCTIONSBOOK - EDUCART PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - LONG ANSWER Type Questions
6 Videos
Similar Questions
Seg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
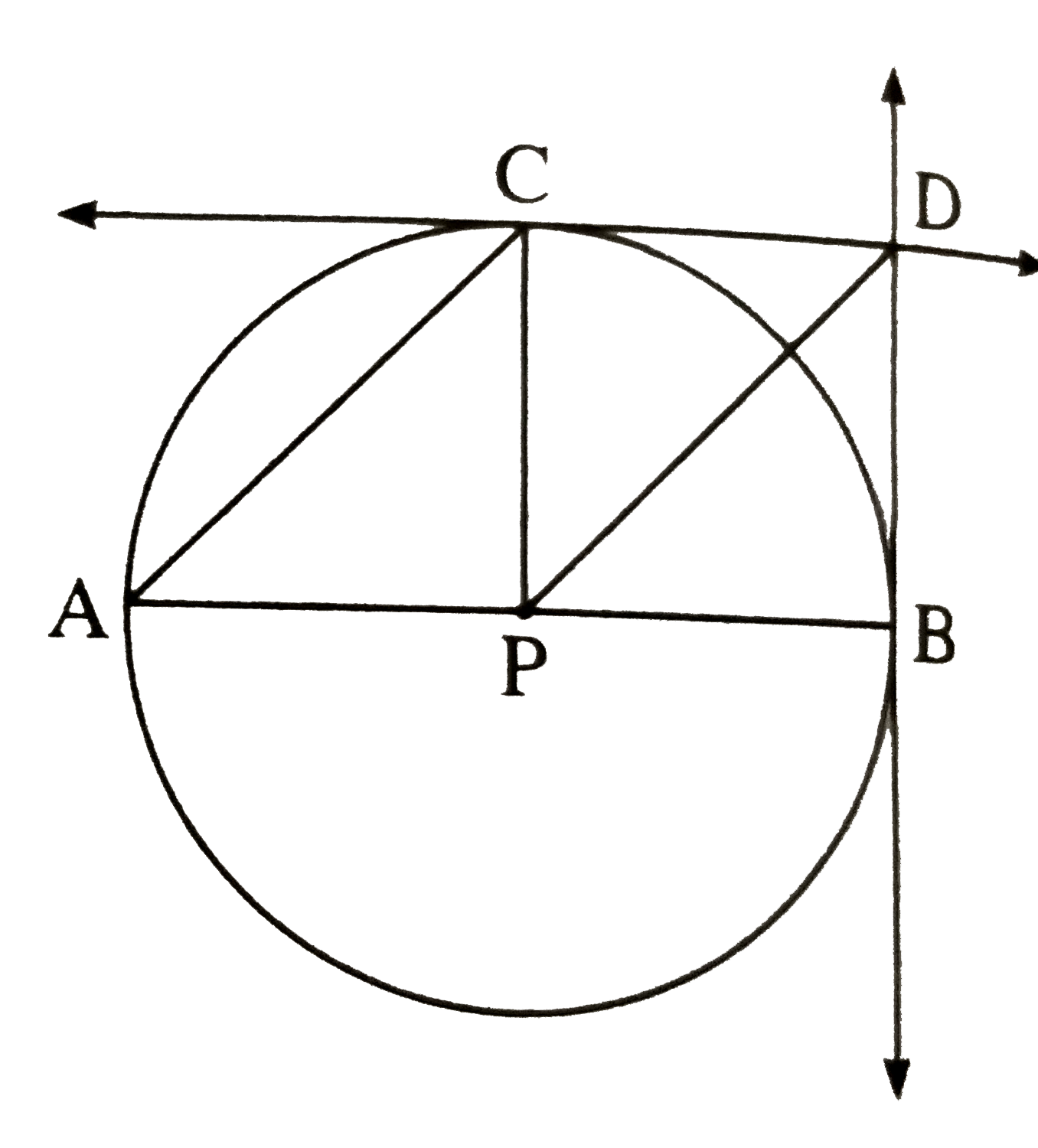
View SolutionIf AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View Solution
Knowledge Check
AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the ∠AEB.
A30∘B60∘C90∘D45∘AD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
A17 cmB15 cmC4 cmD8 cmThere is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
A4.8 cmB10.8cmC9.6 cmDnone of these
AB is diameter of a circle with centre 'O'. CD is a chord which is equal to the radius of the circle. AC and BD are extended so that they intersect each other at point P. Then find the value of ∠APB.
View SolutionAB is the diameter of a circle whose centre is O. DC is a chord of that circle. If DC||AB and ∠BAC=20∘ then ∠ADC=?
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionIn Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to theradius of the circle. AC and BD when extended intersect at a point E. Prove that∠AEB = 60∘
View SolutionIn a circle of radius 5 cm, AB and AC are two chords such that AB=AC=6cm. Find the length of the chord BC
View Solution
