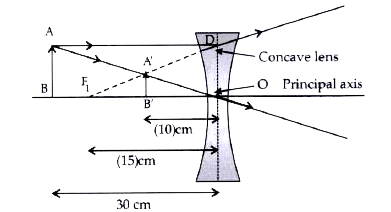
A convceve lens of focal length 15 cm forms an image 10 cm from the lens. How far is the object from the lans ? Draw the ray diagram.
Focal length of concave lens (OF1), f = -15 cm
Image distance, v= -10 cm
According to the lens formula,
1v−1u=1f
1u=1v−1f=−110−1(−15)=−3+230=−130
u=-30 cm
The negative value of u indicates that the object is placed 30 cm in front of the lens. This is shown in the following ray diagram.
Similar Questions
Knowledge Check
A convex lens of focal length 16 cm forms a real image double the size of the object. The image distance of the object from the lens is
A32 cmB24 cmC20 cmD8 cm
A concave (diverging) lens of focal length 15 cm , forms an image 10 cm forms and image 10 cm from the lens . How far is the object placed from the lens ? Draw the ray diagram.
View Solution(i) A diverging lens of focal length 15 cm, forms an image at distance of 10 cm from the lens. How far is the object placed from the lens ?
(ii) Under what condition a diverging lens when placed in a medium behaves as a converging lens
View Solution(a) Draw a ray diagram to show the formation of image of an object placed between infinity and optical centre of a concave lens.
(b) A concave lens of focal length 15 cm forms an image 10 cm from the lens. Calculate (i) the object distance, (ii) the nature and magnification of the image formed.
View SolutionA diverging lens of focal length 15cm forms an image 10cm from the lens. Calculate the distance of the object from the lens, given μ=1.5. What is the linear magnification of the image ?
View SolutionA convex lens of focal length 10 cm is placed at a distance of 12 cm from a wall. How far from the lens should an object be placed so as to form its real image on the wall?
View SolutionA converging lens of focal length 5 cm is placed at a distance of 20 cm from a screen. How far from the lens should an object be placed so as to form its real image on the screen?
View SolutionFind the position of the object of height 5 cm in front of a concave lens of focal length 20 cm to get the image at a distance of 15 cm from the lens. Also find the height and nature of image formed.
View Solution
