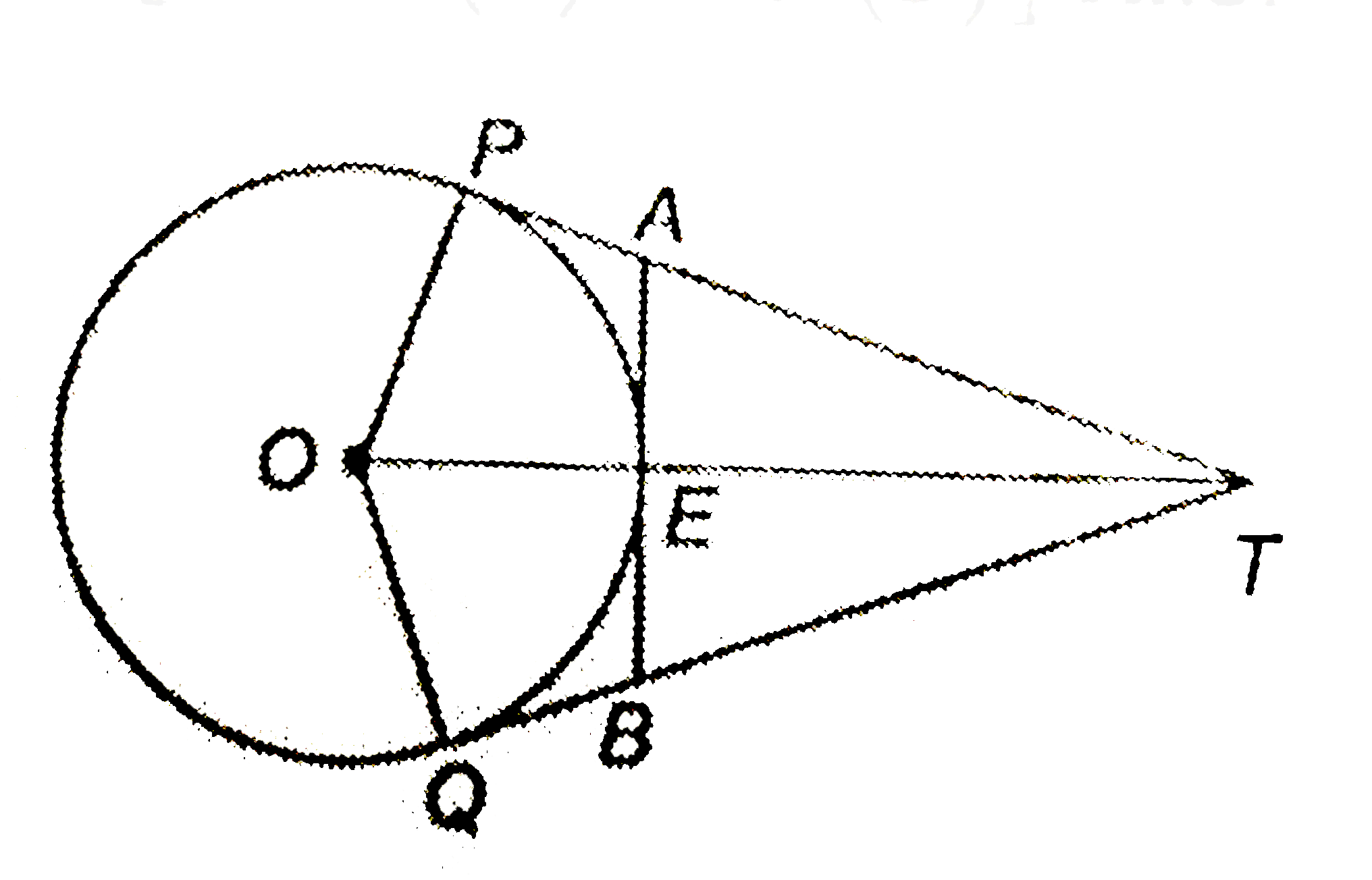
O is the centre of a circle of radius 5cm. T is a point such that OT=1

Type V: O is the center of the circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E . If AB is the tangent to the circle at E; find the length of AB.
A $\frac{10}{3}$
B $\frac{20}{3}$
C $\frac{16}{3}$
DCannot be determined
$O$ is the centre of a circle of radius $5 c m .$ $T$ is a point such that $O T = 13 c m a n d O T$ intersects the circle at $E .$ If $A B$ is the tangent to the circle at $E,$ find length of $A B .$
A20 cm
B $\frac{20}{3} c m$
C $10 c m$
D25 cm
Tangents PT and QT are drawn on a circle of radius 5 cm from point T which is 13 cm away from the circle. What is the length (in cm) of AB?
A $\frac{10}{3} c m$
B $\frac{20}{3} c m$
C $\frac{40}{3} c m$
D $\frac{16}{3} c m$

O is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.