There are red (A), yellow (B) and green (C) tokens in a bag. A : B :: 3 : 8. B : C :: 6 : 13. A : B : C is given by:
9:24:52
3:48:13
3:8:13
3:6:13
To solve the problem of finding the ratio of red (A), yellow (B), and green (C) tokens in a bag, we will follow these steps:
Step 1: Understand the given ratios
We have two ratios provided:
1. A : B = 3 : 8
2. B : C = 6 : 13
Step 2: Express B in terms of A
From the first ratio A : B = 3 : 8, we can express B in terms of A:
- Let A = 3x (for some value x)
- Then, B = 8x/3
Step 3: Express C in terms of B
From the second ratio B : C = 6 : 13, we can express C in terms of B:
- Let B = 6y (for some value y)
- Then, C = 13y/6
Step 4: Set the values of B equal
Since B is expressed in two different ways (from A and from B), we can set them equal to each other:
8x/3 = 6y
Step 5: Solve for y in terms of x
To find a common value, we can solve for y:
- Multiply both sides by 3 to eliminate the fraction:
8x = 18y
- Now, solve for y:
y = 8x/18 = 4x/9
Step 6: Substitute y back to find C in terms of A
Now we substitute y back into the expression for C:
C = 13y/6 = 13(4x/9)/6 = 52x/54 = 26x/27
Step 7: Write the final ratios
Now we have:
- A = 3x
- B = 8x/3
- C = 26x/27
To express A, B, and C in terms of a common variable, we can take the least common multiple (LCM) of the denominators (3 and 27), which is 27.
Step 8: Scale the ratios
- A = 3x = 27 * (3/27)x = 3x
- B = 8x/3 = 27 * (8/81)x = 72x/27
- C = 26x/27 = 26x/27
Step 9: Combine the ratios
Now we can express A : B : C as:
A : B : C = 3x : 8x : 26x = 3 : 8 : 26
Step 10: Simplify the ratios
Now we can simplify the ratios:
A : B : C = 9 : 24 : 52
Final Answer
Thus, the ratio A : B : C is 9 : 24 : 52.
---
We have two ratios provided:
1. A : B = 3 : 8
2. B : C = 6 : 13
From the first ratio A : B = 3 : 8, we can express B in terms of A:
- Let A = 3x (for some value x)
- Then, B = 8x/3
From the second ratio B : C = 6 : 13, we can express C in terms of B:
- Let B = 6y (for some value y)
- Then, C = 13y/6
Since B is expressed in two different ways (from A and from B), we can set them equal to each other:
8x/3 = 6y
To find a common value, we can solve for y:
- Multiply both sides by 3 to eliminate the fraction:
8x = 18y
- Now, solve for y:
y = 8x/18 = 4x/9
Now we substitute y back into the expression for C:
C = 13y/6 = 13(4x/9)/6 = 52x/54 = 26x/27
Now we have:
- A = 3x
- B = 8x/3
- C = 26x/27
- A = 3x = 27 * (3/27)x = 3x
- B = 8x/3 = 27 * (8/81)x = 72x/27
- C = 26x/27 = 26x/27
Now we can express A : B : C as:
A : B : C = 3x : 8x : 26x = 3 : 8 : 26
Now we can simplify the ratios:
A : B : C = 9 : 24 : 52
Thus, the ratio A : B : C is 9 : 24 : 52.
Similar Questions
Knowledge Check
If A:B=5:6 and B:C=8:9, find A:B:C
A20:24:27B30:48:54C20:48:54D40:24:27If a: b= 3 : 5 and b: c = 6 : 2 , find a:b:c
A4:9:45B9:15:5C16:36:20D4:36:20If (a + b) : (b + c) : (c + a) = 6 : 7 : 8 and (a + b + c) = 14, then the value of c is
A6B7C8D14
a+b:b+c:c+a=6:7:8 find a:b:c=?
View SolutionAdd:
3a−4b+4c,2a+3b−8c,a−6b+c
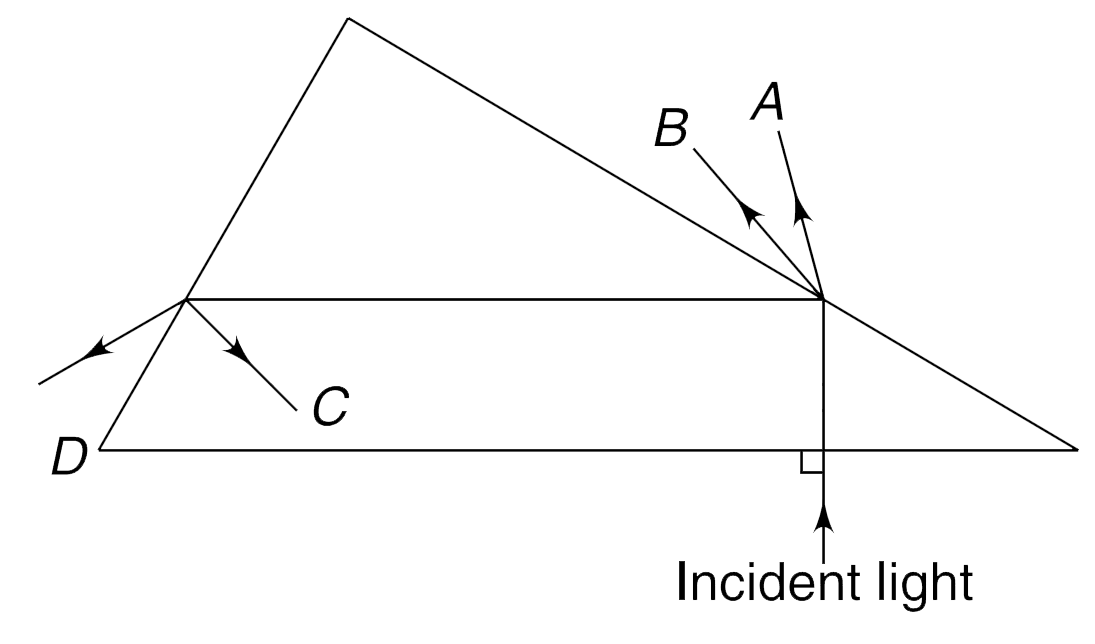
View SolutionWhite light is incident on a glass prism as shown. Four easily identifiable colors – red, green, yellow and blue get separated as A, B, C and D. Which of the rays (A, B, C and D) correspond to which color?
View SolutionIf a: b= 3:5 and b:c = 7:8, then 2a :3b: 8c is equal to
View SolutionIf a : b = 5 : 8 and c : b = 4 : 3, then a : b : c is equal to:
यदि a : b = 5 : 8 और c : b = 4 : 3 है, तो a : b : c किसके बराबर होगा ?
View Solution
