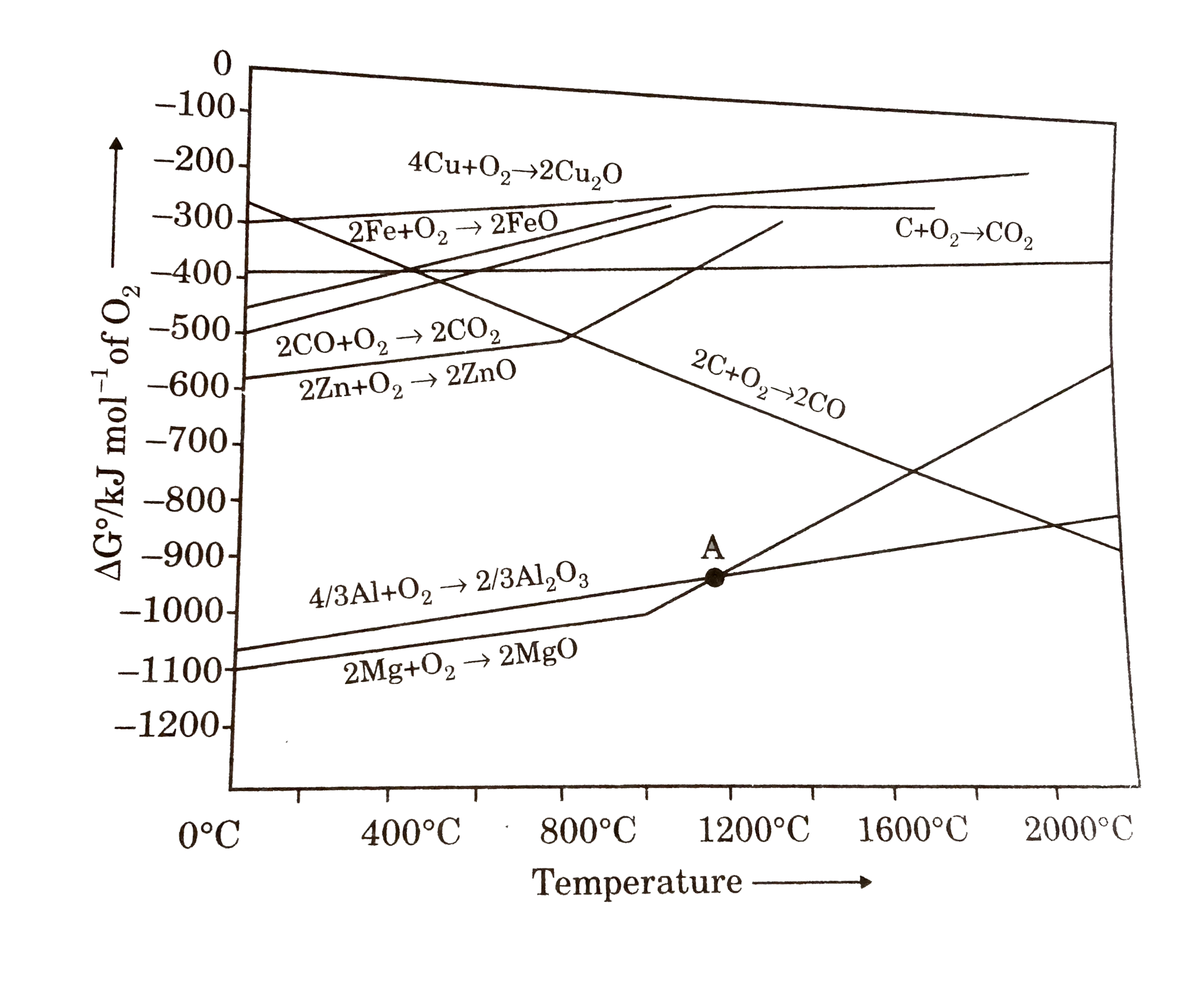
Read each statement carefully and answer the following questions
Which of the following expressions will be true, if the expression
R>O=A>S<T is definitely true.
A
O>T
B
S<R
C
T>A
D
S=O
Video Solution
Text Solution
The correct Answer is:B
Given expression: R>O=A>S><T
Option (a) is not true because we can.t compare O and T.
Option (c) is also not true because we can.t compare T and A.
Option (d) is also not true because O>S. ∴R>SmeansS lt R holds true. Therefore, option (b) is definitely true.
|
Topper's Solved these Questions
- CONCLUSIONS FROM CODED INEQUALITIES AND SYMBOLS Book:LUCENT PUBLICATIONChapter:CONCLUSIONS FROM CODED INEQUALITIES AND SYMBOLS Exercise:Exercise-1
Explore 58 Videos
- COMPARISON ON RANKSBook:LUCENT PUBLICATIONChapter:COMPARISON ON RANKSExercise:Exercise (Type-V: Miscellaneous)
Explore 3 Videos
- CRITICAL REASONINGBook:LUCENT PUBLICATIONChapter:CRITICAL REASONINGExercise:EXERCISE-2
Explore 62 Videos
Similar Questions
Knowledge Check
which of the following expressions will be true if the expression V≤W<R≥N=S≥M is definitely true ?
AR≤VBR=NCR>NDEither R=NorR>NWhich of the following expression is not true ?
A[H+]=[OH−]=√Kw for a neutral solution at all temperatures.B[H+]>√Kwand[OH−]<√Kw for an acidic solutionC[H+]<√Kwand[OH−]>√Kw for an alkaline solutionD[H+]=[OH−]=10−7 M for a neutral solution at all temperature.Which of the following expression is true :-
AH∘f(CO,g)=12ΔH∘f(CO2,g)BΔH∘f(CO,g)=ΔH∘f(C, graphite)+12ΔH∘f(O2,g)CΔH∘f(CO,g)=ΔH∘f(CO2,g)−12ΔH∘f(O,g)DΔH∘f(CO,g)=ΔH∘comb(C, graphite)−ΔH∘comb(CO,g)
Which of the following expressions is true if the expression P<T≤q>S>M≥W is definitely true ?
View SolutionStudy the graph carefully and answer the following questions.
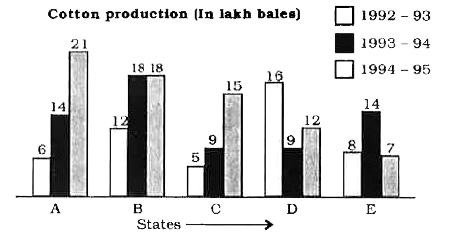
Which of the following statement is false ?
View SolutionWhich of the following expressions is true for an ideal gas ?
View SolutionWhich one of the following will be definitely true if the expression Q<S>V=W≥O≥R is definitely true ?
View SolutionWhich one of the following will be definitely true if the expression D=C≥A>B≥F<G=E≤H is definitely true ?
View Solution