When the remainder obtained by dividing 60606 by 106 is subtracted from the remainder obtained on dividing 70707 by 107, then the resultant number is
7
8
5
8
The correct Answer is:A
To solve the problem, we need to find the remainders of two divisions and then subtract one from the other. Here’s a step-by-step breakdown of the solution:
Step 1: Find the remainder of 60606 when divided by 106.
To do this, we perform the division:
1. Divide 60606 by 106:
- Calculate how many times 106 fits into 60606.
- 106 goes into 60606 approximately 572 times (since 106×572=60632 which is too high, we try 571).
- 106×571=60526.
2. Calculate the remainder:
- Subtract 60526 from 60606:
60606−60526=80
So, the remainder when 60606 is divided by 106 is 80.
Step 2: Find the remainder of 70707 when divided by 107.
Now, we perform the division for the second number:
1. Divide 70707 by 107:
- Calculate how many times 107 fits into 70707.
- 107 goes into 70707 approximately 660 times (since 107×660=70620).
2. Calculate the remainder:
- Subtract 70620 from 70707:
70707−70620=87
So, the remainder when 70707 is divided by 107 is 87.
Step 3: Subtract the two remainders.
Now, we subtract the remainder obtained from the first division from the remainder obtained from the second division:
87−80=7
Conclusion:
The resultant number after performing the operations is 7.
---
To do this, we perform the division:
- Calculate how many times 106 fits into 60606.
- 106 goes into 60606 approximately 572 times (since 106×572=60632 which is too high, we try 571).
- 106×571=60526.
- Subtract 60526 from 60606:
60606−60526=80
So, the remainder when 60606 is divided by 106 is 80.
Now, we perform the division for the second number:
- Calculate how many times 107 fits into 70707.
- 107 goes into 70707 approximately 660 times (since 107×660=70620).
2. Calculate the remainder:
- Subtract 70620 from 70707:
70707−70620=87
So, the remainder when 70707 is divided by 107 is 87.
Now, we subtract the remainder obtained from the first division from the remainder obtained from the second division:
The resultant number after performing the operations is 7.
Similar Questions
Knowledge Check
When the remainder obtained on dividing 80808 by 108 is divided by the remainder obtained on dividing 90909 by 109, then the quotient is
A8B12C3D6The remainder obtained when 5125 is divided by 13 is
A3B7C12D11When
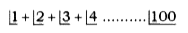 , is divided by 5, the remainder obtained is ?A0B1C2D3
, is divided by 5, the remainder obtained is ?A0B1C2D3
When
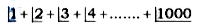 is divided by 12, the remainder obtained is?
is divided by 12, the remainder obtained is?
View SolutionWhen
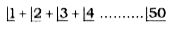 , is divided by 12, the remainder obtained is ?
, is divided by 12, the remainder obtained is ?
View SolutionWhen 221 is divided by 9, the remainder obtained is ?
View SolutionWhen 1177 is divided by 7, the remainder obtained is ?
View SolutionWhen 740 is divided by 400, the remainder obtained is ?
View Solution

 is divided by 10, the remaindeer obtained is ?
is divided by 10, the remaindeer obtained is ?