Question

In a group of 15 people, 7 read French, 8 read English while 3 of them read none of these two. How many of them read French and English both?

Options

A. 0
B. 3
C. 4
D. 5

Answer

B

Explanation

Let circles F and E represent persons who read French and English respectively.

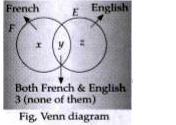
According to the question persons who read French = `x + y = 7 .....(i)`
Persons who read English = `y + z = 8 ... (ii) `
Now, `(x + y + z) + 3 = 15 `
or, `x + y + z = 12 ... (iii) `
[`because` Total no. of persons = 15]
Adding (i) & (ii), we get
`x + 2y + z = 15`
Subtracting (iii) from (iv). we get
`y = 15 - 12 = 3 `
Therefore, required number of persons who read French and English both = `y = 3`.