Two identical calls send the same current in 2Ω resistance, whether connected in series or in parallel. The internal resistance of the cell should be
1Ω
2Ω
0.5Ω
2.5Ω
The correct Answer is:B
Given, lseries=lparallel
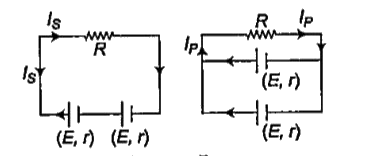
ls=E+Er+r+R=2E2r+R
lp=Er2+R=2Er+2R
Since, ls=lp
2E2r+R=2Er+2R
⇒ 2r+R=r+2R
⇒ r=R
⇒ r=2Ω
Similar Questions
Five identical cells each of internal resistance 1Ω and emf 5V are connected in series and in parallel with an external resistance 'R' . For what value of 'R', current in series and parallel combination will remain the same ?
View SolutionThree identical cells of emf 4V with 1Ω internal resistance each are connected in series to an external resistance of 6Ω. Find the current flowing in the circuit.
View Solution
Knowledge Check
Two identical calls send the same current in 2Ω resistance, whether connected in series of in parallel. The internal resistance of the cell should be
A1ΩB2ΩC12ΩD2.5ΩTwo identical calls send the same current in 2Ω resistance, whether connected in series or in parallel. The internal resistance of the cell should be
A1ΩB2ΩC0.5ΩD2.5ΩTwo identical cells send the same current in 2Ω resistance, whether connected in series or in parallel with each other. The internal resistance of cell should be
A1ΩB2ΩC0.5ΩD2.5Ω
Four identical cells with 1.5Ω internal resistance each are connected in parallel to an external resistance of 5Ω. What should be the value of the emf of each cell to drive a current of 4 A in the circuit ?
View SolutionTwo coils have a combined resistance of 9Ω when connected in series and 2Ω when connected in parallel. Find the resistance of each coil.
View SolutionA circuit consists of a resistance R connected to n similar cells. If the current in the circuit is the same whether the cells are connected in series or in parallel, then the internal resistancer of each cell is given by
View SolutionThree similar cells, each of emf 2 V and internal resistance rΩ send the same current through an external resistance of 2Ω, when connected in series or in parallel. The strength of the current flowing through the external resistance is
View SolutionTwo batteries each of E and internal resistance r are connected turn by turn in series and in parallel, and are used to find current in an external resistance R. If the current in series is equal to that in parallel, the internal resistance of each battery is
View Solution
