There are 20 vehicles-cars and motor cycles in a parking area. If there are 56 wheels together, how many cars are there?
8
10
12
20
The correct Answer is:A
To solve the problem, we need to find out how many cars are in the parking area given the total number of vehicles and wheels. Let's break it down step by step.
Step 1: Define Variables
Let:
- x = number of cars
- y = number of motorcycles
Step 2: Set Up Equations
From the problem, we know:
1. The total number of vehicles (cars and motorcycles) is 20:
x+y=20(Equation 1)
2. The total number of wheels is 56. Since cars have 4 wheels and motorcycles have 2 wheels, we can express this as:
4x+2y=56(Equation 2)
Step 3: Solve Equation 1 for one variable
From Equation 1, we can express y in terms of x:
y=20−x
Step 4: Substitute into Equation 2
Now, substitute y in Equation 2:
4x+2(20−x)=56
Expanding this gives:
4x+40−2x=56
Step 5: Simplify the Equation
Combine like terms:
2x+40=56
Step 6: Isolate x
Subtract 40 from both sides:
2x=56−40
2x=16
Step 7: Solve for x
Divide both sides by 2:
x=162=8
Step 8: Conclusion
Thus, the number of cars x is 8.
Let:
- x = number of cars
- y = number of motorcycles
From the problem, we know:
1. The total number of vehicles (cars and motorcycles) is 20:
x+y=20(Equation 1)
4x+2y=56(Equation 2)
From Equation 1, we can express y in terms of x:
y=20−x
Now, substitute y in Equation 2:
4x+2(20−x)=56
Expanding this gives:
4x+40−2x=56
Combine like terms:
2x+40=56
Subtract 40 from both sides:
2x=56−40
2x=16
Divide both sides by 2:
x=162=8
Thus, the number of cars x is 8.
Topper's Solved these Questions
- SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 1EXERCISE - SECTION C
10 Videos
- SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 1EXERCISE - Section -A
20 Videos
- SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 1EXERCISE - Section -C
10 Videos
- SAMPLE PAPER 07BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 07EXERCISE - SECTION -C
10 Videos
- SAMPLE PAPER 10BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 10EXERCISE - SECTION-C
10 Videos
Similar Questions
Knowledge Check
In a row of cars, blue car is at the bottom end. There are 18 cars between yellow and blue car. There are 8 cars between red and blue car. If there are 6 cars above yellow car, then how many minimum cars are there in the row?
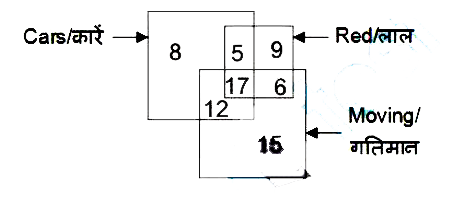
A34B26C32D35In the given figure, how many moving cars are not red?
 A22B17C12D29
A22B17C12D291116 of the residents of a housing society own cars and 2033 of the car owners have purchased covered parking space. IF 130 of the residents parked in the open, how many residents when there in the society
AA. 400BB. 480CC. 384DD. 320
There are 14 lines in a car parking. There are 420 places for parking the cars in each line. How many cars can be parked in the car parking ?
View SolutionThere are 47 cars in a row. Black car is 18th from right end and white car is 39th from right end. How many cars are there between black and white car?
View SolutionThe Bar graph given below presents the number of cars parked on ten different days in a parking area
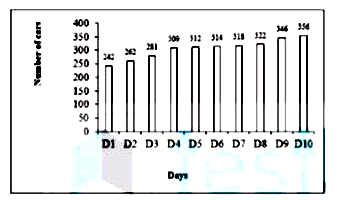
What is the total number of cars parked on all the ten days in the parking area ?
View SolutionThirty six vehicles are parked in a parking lot in a single row. After the first car, there is one scooter, after second car there are three scooters and so on. Work out the number of scooters in the second half of the row ?
View SolutionThe Bar graph given below presentes the number of cars parked on ten different days in a parking area.
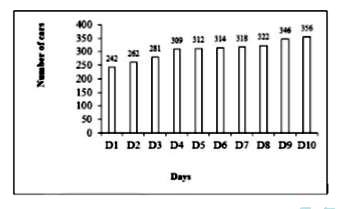
What is the difference in the number of cars parked on D3 and D8 ?
View Solution