Question

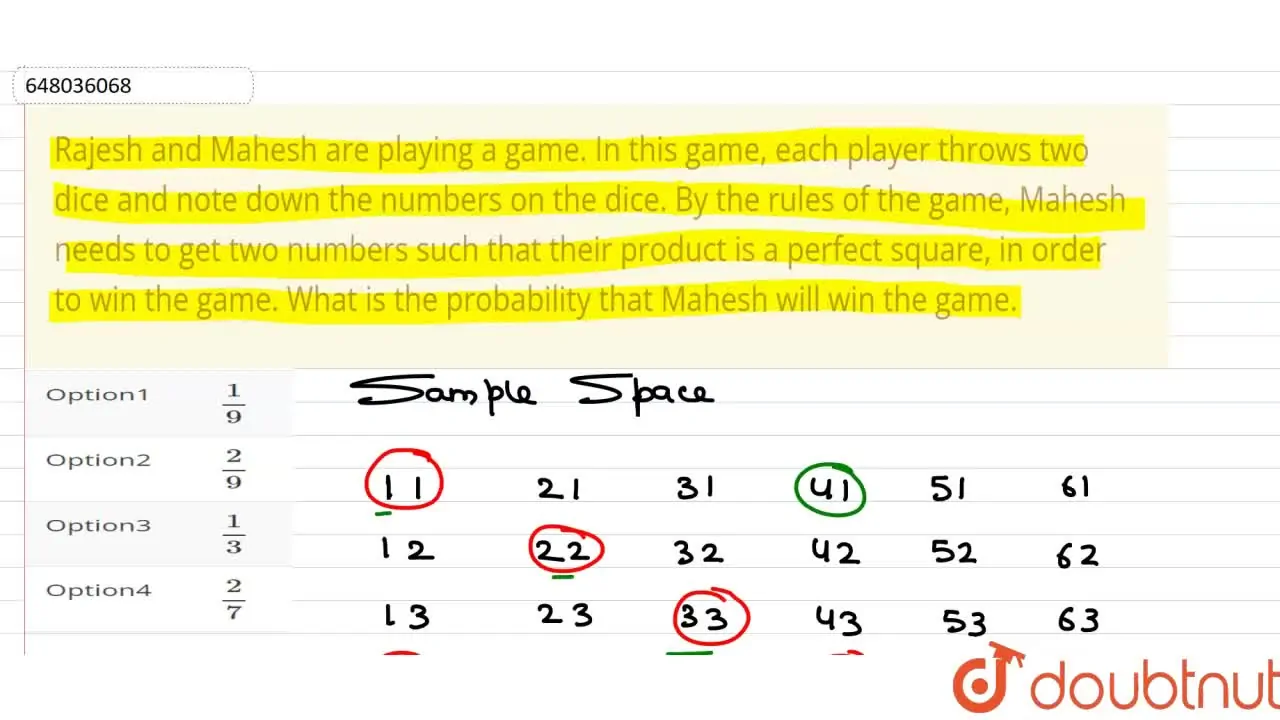
Rajesh and Mahesh are playing a game. In this game, each player throws two dice and note down the numbers on the dice. By the rules of the game, Mahesh needs to get two numbers such that their product is a perfect square, in order to win the game. What is the probability that Mahesh will win the game.

Options

A. `1/9`
B. `2/9`
C. `1/3`
D. `2/7`

Answer

B

Explanation

To find the probability that Mahesh will win the game by rolling two dice such that their product is a perfect square, we can follow these steps:

Step 1: Determine the Sample Space
When two dice are thrown, each die has 6 faces. Therefore, the total number of outcomes when rolling two dice is:

\( \text{Total outcomes} = 6 \times 6 = 36 \)

Step 2: Identify Perfect Squares
A perfect square is a number that can be expressed as the square of an integer. The perfect squares that can be formed with the products of two numbers from 1 to 6 (the faces of the dice) are:

- \(1 = 1 \times 1\)
- \(4 = 2 \times 2\)
- \(9 = 3 \times 3\)
- \(16 = 4 \times 4\)
- \(25 = 5 \times 5\)
- \(36 = 6 \times 6\)

We need to find pairs of numbers (from 1 to 6) whose product is one of these perfect squares.

Step 3: List the Pairs that Yield Perfect Squares
We will check the products of all combinations of the numbers from the two dice:

1. Product = 1: (1, 1)
2. Product = 4: (1, 4), (2, 2), (4, 1)
3. Product = 9: (3, 3)
4. Product = 16: (4, 4)
5. Product = 25: (5, 5)
6. Product = 36: (6, 6)

Now let's count the valid pairs:

- For product = 1: (1, 1) → 1 way
- For product = 4: (1, 4), (4, 1), (2, 2) → 3 ways
- For product = 9: (3, 3) → 1 way
- For product = 16: (4, 4) → 1 way
- For product = 25: (5, 5) → 1 way
- For product = 36: (6, 6) → 1 way

Step 4: Count the Total Successful Outcomes
Now, we will sum the total number of successful outcomes:

\( \text{Total successful outcomes} = 1 + 3 + 1 + 1 + 1 + 1 = 8 \)

Step 5: Calculate the Probability
The probability \(P\) that Mahesh will win the game is given by the ratio of successful outcomes to the total outcomes:

\( P = \frac{\text{Number of successful outcomes}}{\text{Total outcomes}} = \frac{8}{36} = \frac{2}{9} \)

Final Answer
Thus, the probability that Mahesh will win the game is:

\( \boxed{\frac{2}{9}} \)

---