Question

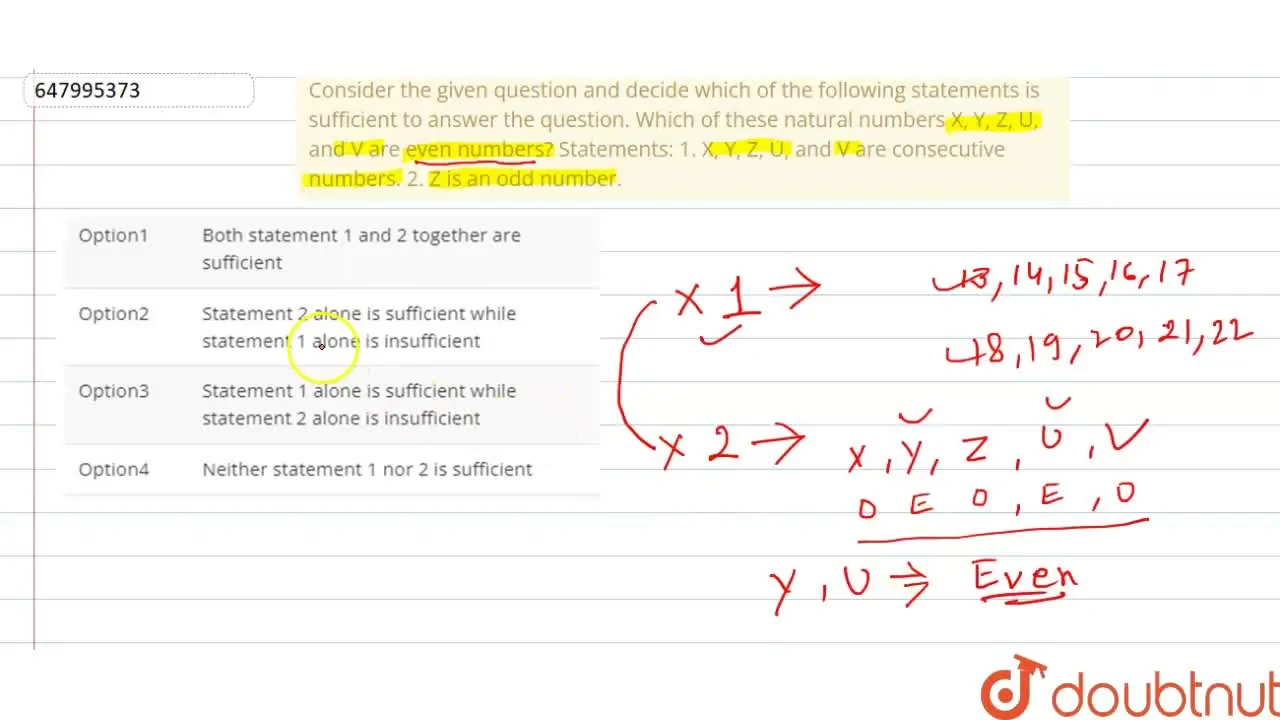
Consider the given question and decide which of the following statements is sufficient to answer the question.
Which of these natural numbers X, Y, Z, U, and V are even numbers?
Statements:
1. X, Y, Z, U, and V are consecutive numbers.
2. Z is an odd number.

Options

A. Both statement 1 and 2 together are sufficient
B. Statement 2 alone is sufficient while statement 1 alone is insufficient
C. Statement 1 alone is sufficient while statement 2 alone is insufficient
D. Neither statement 1 nor 2 is sufficient

Explanation

To determine which of the natural numbers X, Y, Z, U, and V are even numbers based on the provided statements, we can analyze each statement step by step.

Step 1: Analyze Statement 1
Statement 1: X, Y, Z, U, and V are consecutive numbers.

Consecutive numbers can be represented as:
- If we start with an arbitrary number \( n \), the numbers can be represented as \( n, n+1, n+2, n+3, n+4 \).

This means that:
- If \( n \) is even, then \( n \) and \( n+2, n+4 \) are even, while \( n+1, n+3 \) are odd.
- If \( n \) is odd, then \( n \) and \( n+2, n+4 \) are odd, while \( n+1, n+3 \) are even.

Since we do not know the starting number \( n \), we cannot definitively determine which of X, Y, Z, U, and V are even or odd based solely on this statement.

Conclusion for Statement 1: Not sufficient.

Step 2: Analyze Statement 2
Statement 2: Z is an odd number.

If Z is odd, we can represent the five consecutive numbers as:
- If Z is odd, then we can express the numbers as follows:
- Let’s say \( Z = n \) (where \( n \) is odd), then:
- \( X = n-2 \) (even)
- \( Y = n-1 \) (even)
- \( Z = n \) (odd)
- \( U = n+1 \) (even)
- \( V = n+2 \) (odd)

From this, we can identify that:
- The even numbers are X, Y, and U.

Conclusion for Statement 2: Sufficient to determine that X, Y, and U are even.

Step 3: Combine Statements
Combining both statements:
- From Statement 1, we know the numbers are consecutive.
- From Statement 2, we know Z is odd.

Thus, we can conclude:
- If Z is odd, then the even numbers among X, Y, Z, U, and V will be Y and U.

Final Conclusion: Both statements together are sufficient to determine which numbers are even.

Summary of the Solution:
- Statement 1 alone: Not sufficient.
- Statement 2 alone: Sufficient.
- Both statements together: Sufficient.