Give the expression to find out the displacement of a particle in nth second.
To find the expression for the displacement of a particle in the nth second, we can follow these steps:
1. Understand the Concept:
The displacement of a particle in the nth second can be calculated by finding the difference in displacement between the end of the nth second and the end of the (n-1)th second.
2. Define the Displacement:
Let Sn be the displacement of the particle from the start to the end of the nth second, and Sn−1 be the displacement from the start to the end of the (n-1)th second. The displacement in the nth second, S(nth)n, can be expressed as:
S(nth)n=Sn−Sn−1
3. Use the Displacement Formula:
The formula for displacement under uniform acceleration is given by:
S=ut+12at2
where u is the initial velocity, a is the acceleration, and t is the time.
4. Calculate Sn:
For the nth second, we substitute t=n:
Sn=un+12an2
5. Calculate Sn−1:
For the (n-1)th second, we substitute t=n−1:
Sn−1=u(n−1)+12a(n−1)2
6. Substitute into the Displacement Formula:
Now we substitute Sn and Sn−1 into the equation for S(nth)n:
S(nth)n=(un+12an2)−(u(n−1)+12a(n−1)2)
7. Simplify the Expression:
Expanding Sn−1:
Sn−1=u(n−1)+12a(n2−2n+1)=u(n−1)+12an2−an+12a
Now substituting this back:
S(nth)n=un+12an2−(u(n−1)+12an2−an+12a)
Simplifying this gives:
S(nth)n=u+12a(2n−1)
8. Final Expression:
Thus, the expression for the displacement of a particle in the nth second is:
S(nth)n=u+a2(2n−1)
The displacement of a particle in the nth second can be calculated by finding the difference in displacement between the end of the nth second and the end of the (n-1)th second.
Let Sn be the displacement of the particle from the start to the end of the nth second, and Sn−1 be the displacement from the start to the end of the (n-1)th second. The displacement in the nth second, S(nth)n, can be expressed as:
S(nth)n=Sn−Sn−1
The formula for displacement under uniform acceleration is given by:
S=ut+12at2
where u is the initial velocity, a is the acceleration, and t is the time.
For the nth second, we substitute t=n:
Sn=un+12an2
For the (n-1)th second, we substitute t=n−1:
Sn−1=u(n−1)+12a(n−1)2
Now we substitute Sn and Sn−1 into the equation for S(nth)n:
S(nth)n=(un+12an2)−(u(n−1)+12a(n−1)2)
Expanding Sn−1:
Sn−1=u(n−1)+12a(n2−2n+1)=u(n−1)+12an2−an+12a
Now substituting this back:
S(nth)n=un+12an2−(u(n−1)+12an2−an+12a)
Simplifying this gives:
S(nth)n=u+12a(2n−1)
Thus, the expression for the displacement of a particle in the nth second is:
S(nth)n=u+a2(2n−1)
Topper's Solved these Questions
- DESCRIPTION OF MOTIONBOOK - CENGAGE PHYSICSCHAPTER - DESCRIPTION OF MOTIONEXERCISE - MANDATORY EXERCISE (EXERCISE SET - II)
7 Videos
- DESCRIPTION OF MOTIONBOOK - CENGAGE PHYSICSCHAPTER - DESCRIPTION OF MOTIONEXERCISE - MANDATORY EXERCISE (EXERCISE SET - III)
12 Videos
- DESCRIPTION OF MOTIONBOOK - CENGAGE PHYSICSCHAPTER - DESCRIPTION OF MOTIONEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISE
10 Videos
- ELASTICITYBOOK - CENGAGE PHYSICSCHAPTER - ELASTICITYEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
Knowledge Check
Accleration vs time graph of a particle starting from rest is given. Find the displacement of particle in first 2 seconds.
 A38B83C43D316
A38B83C43D316The velocity - time graph of a particle moving along a straight line is shown in the figure given below
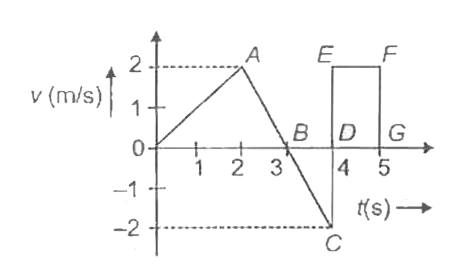
The displacement of the particle in 5 second isA0.5 mB1 mC2 mD4 mFigure shows the position time graph for a particle in one dimensional motion. What is the displacement of the particle in first 4 seconds ?
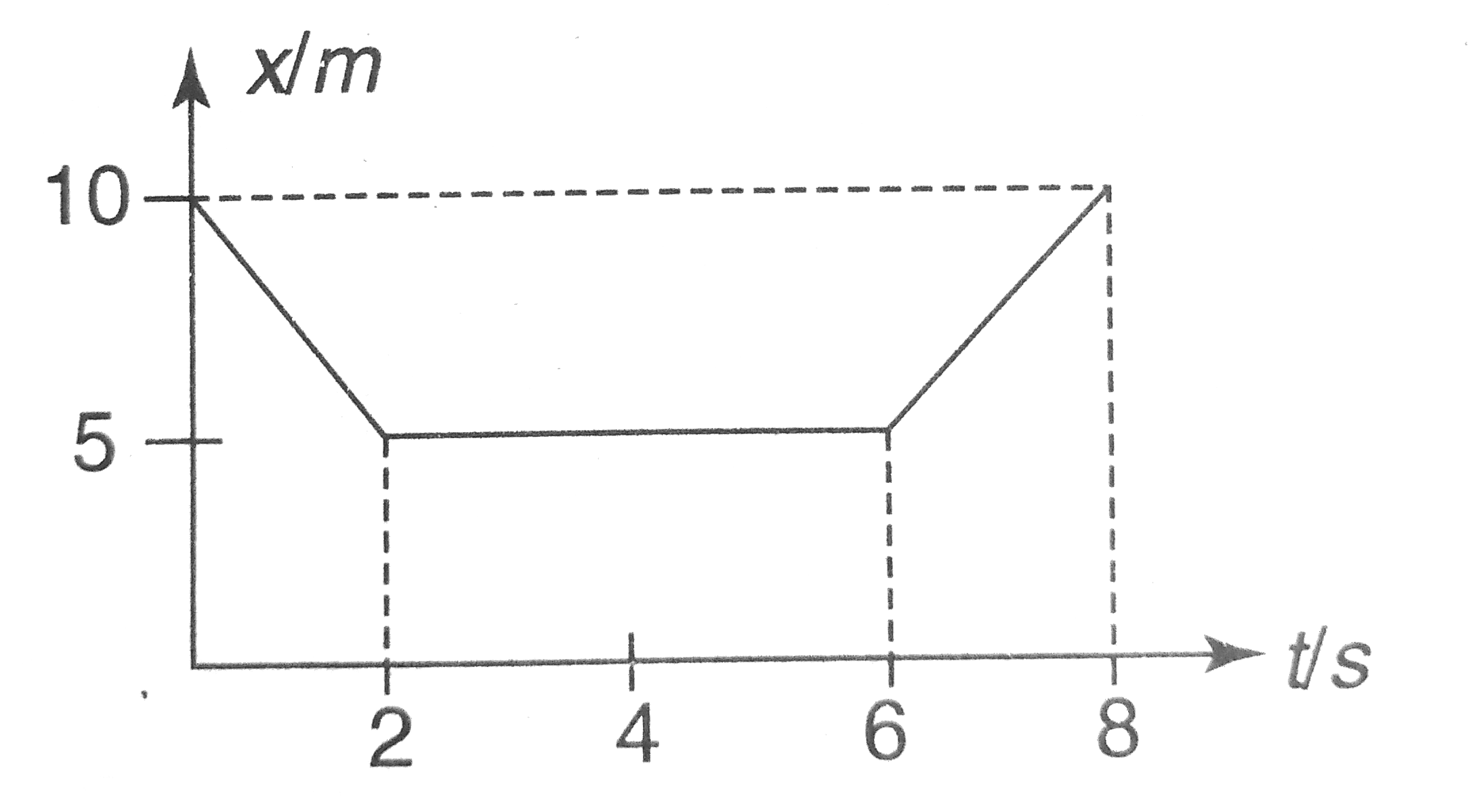 A5 mB−5mCzeroD15 m
A5 mB−5mCzeroD15 m
If v=3t2−2t+5, where v is velocity (in m/s) and t is time (in second). Find the displacement (in m) of particle in third second.
(A) 19
(B) 24
(C) 9
(D) None of these
View SolutionAssuming the general expression for the displacement of a particle performing SHM, obtain the expressions for its velocity and acceleration as functions of the displacement.
View SolutionA particle starts moving from rest such that it has uniform acceleration a0 during the 1st second of motion, uniform acceleration a02 during the 2nd second of motion, uniform acceleration a04 during the 3rd second of motion, and so on, such that it has uniform acceleration a02n−1 during the nth second of motion If the displacement of the particle during the 5th second of motion isD5=Ka032 , the value of K is
View SolutionThe velocity of a particle moving in a straight path is given by u=16t−4t2 where u and t are measured in ft/s and second units respectively. If the initial displacement be 10 ft, find the displacement of the particle in t seconds.
View SolutionThe periodic time of a linear harmonic oscillator is 2π second, with maximum displacement of 1cm. If the particle starts from extreme position, find the displacement of the particle after π3 seconds.
View Solution
