Suppose y'+y=0. Which of the following is a possibility for y=f(x)
y=tanx
y=secx
y=sinx
y=1x,x≠0
The correct Answer is:C
To solve the differential equation y′+y=0 and determine which of the given options for y=f(x) is a possibility, we will analyze each option step by step.
Step 1: Analyze Option 1: y=tanx
1. Find the derivative:
y′=ddx(tanx)=sec2x
2. Substitute into the equation:
y′+y=sec2x+tanx
3. Set the equation to zero:
sec2x+tanx=0
4. Rewrite in terms of sine and cosine:
1cos2x+sinxcosx=0
1+sinxcosxcos2x=0
5. Solve for sinxcosx:
1+sinxcosx=0⟹sinxcosx=−1
This is impossible since sinxcosx can only take values in the range (−1/2,1/2).
Conclusion: Option 1 is not possible.
Step 2: Analyze Option 2: y=secx
1. Find the derivative:
y′=ddx(secx)=secxtanx
2. Substitute into the equation:
y′+y=secxtanx+secx
3. Factor out secx:
secx(tanx+1)=0
4. Set the equation to zero:
tanx+1=0⟹tanx=−1
This is possible for values of x such as x=3π4+nπ.
Conclusion: Option 2 is possible.
Step 3: Analyze Option 3: y=sinx
1. Find the derivative:
y′=ddx(sinx)=cosx
2. Substitute into the equation:
y′+y=cosx+sinx
3. Set the equation to zero:
cosx+sinx=0⟹sinx=−cosx
4. Solve for x:
tanx=−1
This is possible for values of x such as x=3π4+nπ.
Conclusion: Option 3 is possible.
Step 4: Analyze Option 4: y=1x
1. Find the derivative:
y′=ddx(1x)=−1x2
2. Substitute into the equation:
y′+y=−1x2+1x
3. Set the equation to zero:
−1x2+1x=0
4. Solve for x:
1x=1x2⟹x=1
This is possible at x=1.
Conclusion: Option 4 is possible.
Final Conclusion:
The possible options for y=f(x) are Option 2, Option 3, and Option 4.
---
y′=ddx(tanx)=sec2x
2. Substitute into the equation:
y′+y=sec2x+tanx
3. Set the equation to zero:
sec2x+tanx=0
1cos2x+sinxcosx=0
1+sinxcosxcos2x=0
1+sinxcosx=0⟹sinxcosx=−1
This is impossible since sinxcosx can only take values in the range (−1/2,1/2).
y′=ddx(secx)=secxtanx
y′+y=secxtanx+secx
secx(tanx+1)=0
tanx+1=0⟹tanx=−1
This is possible for values of x such as x=3π4+nπ.
y′=ddx(sinx)=cosx
y′+y=cosx+sinx
cosx+sinx=0⟹sinx=−cosx
tanx=−1
This is possible for values of x such as x=3π4+nπ.
y′=ddx(1x)=−1x2
y′+y=−1x2+1x
−1x2+1x=0
1x=1x2⟹x=1
This is possible at x=1.
The possible options for y=f(x) are Option 2, Option 3, and Option 4.
Topper's Solved these Questions
Similar Questions
If the line 3x−4y−λ=0 touches the circle x2+y2−4x−8y−5=0 at (a, b) then which of the following is not the possible value of λ+a+b?
View SolutionSuppose that a function f satisfies the following conditions for all real vaues of x and y
(i) f(x+y)=f(x).f(y)
(ii) f(x)=1+xg(x), where limx→0g(x)=2. The value of logf(5) is
View Solution
Knowledge Check
The following figure shows the graphs of a differentiable fucntion y=f(x) on the interval [a,b] (not contaning 0).
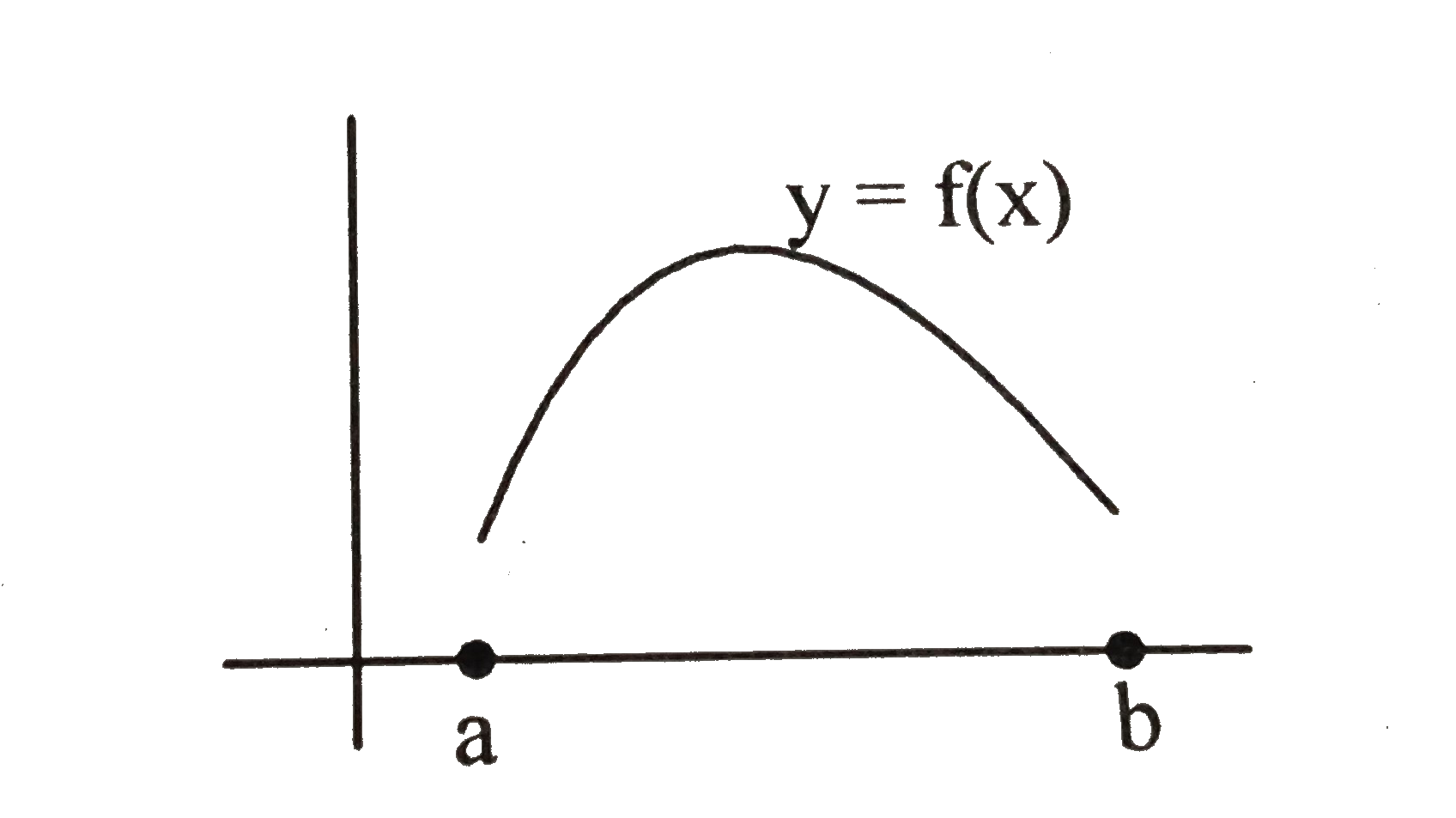
Let g(x)=f(x)/x which of the following is a possible graph of y=g(x) ?A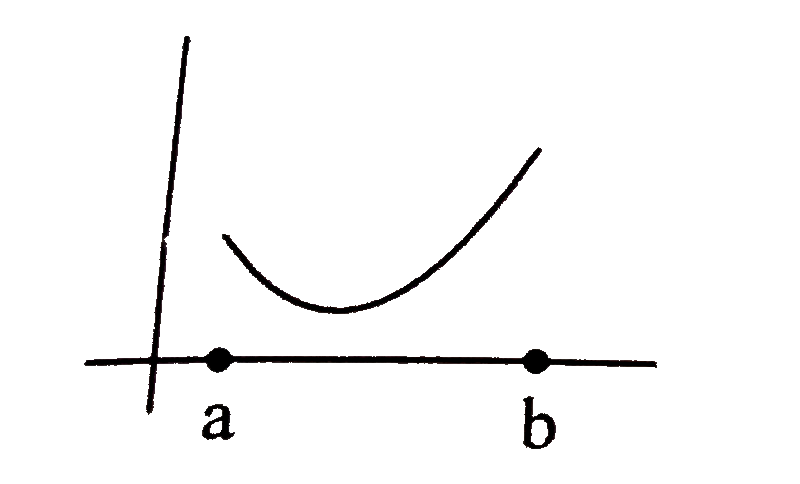 B
B C
C D
D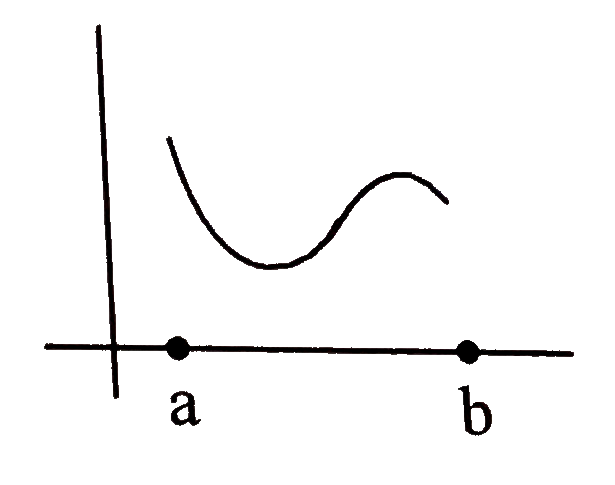
If f:R→(0,∞)be a differentiable function f(x) satisfying
f(x+y)−f(x−y)=f(x)⋅{f(y)−f(y)−y},∀x,y∈R,(f(y)≠f(−y) for all y∈R) and f'(0)=2010.
Now, answer the following questions.
Which of the following is true for f(x)Af(x) is one-one and intoB{f(x)} is non-periodic, where {⋅} denotes fractional part of x.Cf(x)=4 has only two solutions.Df(x)=f−1(x) has only one solution .Which of the following functions satisfies the condition
f(x+yx−y)=f(x)+f(y)f(x)−f(y)?Af(x)=xBf(x)=ax+bCf(x)=2xDf(x)=x2
Consider a differentiable function f:R→R for which f'(0)=ln2andf(x+y)=2xf(y)+4yf(x)∀x,y∈R which of the following is /are correct?
View SolutionA decimal number 'm' (say) can be expressed as
m=1+D
where l→ integer part
and D→ decimal part, 0≤D<1
and [m]= greatest integer less than or equal to m if 0<D<0.5
Hence, f(x,y)=⎧⎪⎨⎪⎩[x+y]if0<D<0.5{x+y}if0.5≤D<1(x+y) otherwise
Also, F(f(x,y))=−f(x,y)
and G(f(x,y))=−F(f(x,y))
Which of the following expressions will yeild a number which has a positive integral square root if if x, y are positive
View SolutionIf ∣∣ ∣ ∣∣xy00xyy0x∣∣ ∣ ∣∣=0, then which one of the following is correct ?
View SolutionA decimal number 'm' (say) can be expressed as
m=1+D
where l→ integer part
and D→ decimal part, 0≤D<1
and [m]= greatest integer less than or equal to m if 0<D<0.5
Hence, f(x,y)=⎧⎪⎨⎪⎩[x+y]if0<D<0.5{x+y}if0.5≤D<1(x+y) otherwise
Also, F(f(x,y))=−f(x,y)
and G(f(x,y))=−F(f(x,y))
Which of the following statements is true if x and y are positive ?
View SolutionIf x+y>5 and x−y>3, then which of the following inequalities gives all the possible values of x ?
View Solution

