The volume of a conical frustum and that of a cylinder are same. The height of the cylinder is 1/3 m and radius is 62 m. The height of the frustum is 31 m and the radius of one end is 10 m. Find the radius of the other end.
To solve the problem, we need to find the radius of the other end of a conical frustum given that its volume is equal to that of a cylinder. Let's break down the solution step by step.
Step 1: Find the volume of the cylinder
The formula for the volume V of a cylinder is given by:
V=πr2h
where r is the radius and h is the height.
Given:
- Radius of the cylinder r=62 m
- Height of the cylinder h=13 m
Substituting the values into the formula:
Vcylinder=π(62)2(13)
Calculating this:
Vcylinder=π⋅3844⋅13=3844π3 m3
Step 2: Write the volume formula for the conical frustum
The volume V of a conical frustum is given by:
V=13πh(r21+r22+r1r2)
where h is the height, r1 is the radius of one end, and r2 is the radius of the other end.
Given:
- Height of the frustum h=31 m
- Radius of one end r1=10 m
- Radius of the other end r2=r (unknown)
Substituting the known values into the formula:
Vfrustum=13π(31)(102+r2+10r)
Calculating:
Vfrustum=13π(31)(100+r2+10r)
Step 3: Set the volumes equal to each other
Since the volumes of the cylinder and the frustum are equal:
3844π3=13π(31)(100+r2+10r)
Step 4: Simplify the equation
We can cancel 13π from both sides:
3844=31(100+r2+10r)
Expanding the right side:
3844=3100+31r2+310r
Step 5: Rearranging the equation
Rearranging gives:
31r2+310r+3100−3844=0
31r2+310r−744=0
Step 6: Dividing the entire equation by 31
To simplify, divide the entire equation by 31:
r2+10r−24=0
Step 7: Factor the quadratic equation
Now we need to factor the quadratic:
(r+12)(r−2)=0
Step 8: Solve for r
Setting each factor to zero gives us:
r+12=0⇒r=−12(not valid since radius cannot be negative)
r−2=0⇒r=2
Conclusion
The radius of the other end of the conical frustum is:
2 m
The formula for the volume V of a cylinder is given by:
V=πr2h
where r is the radius and h is the height.
- Radius of the cylinder r=62 m
- Height of the cylinder h=13 m
Vcylinder=π(62)2(13)
Calculating this:
Vcylinder=π⋅3844⋅13=3844π3 m3
The volume V of a conical frustum is given by:
V=13πh(r21+r22+r1r2)
where h is the height, r1 is the radius of one end, and r2 is the radius of the other end.
- Height of the frustum h=31 m
- Radius of one end r1=10 m
- Radius of the other end r2=r (unknown)
Vfrustum=13π(31)(102+r2+10r)
Calculating:
Vfrustum=13π(31)(100+r2+10r)
Since the volumes of the cylinder and the frustum are equal:
3844π3=13π(31)(100+r2+10r)
We can cancel 13π from both sides:
3844=31(100+r2+10r)
Expanding the right side:
3844=3100+31r2+310r
Rearranging gives:
31r2+310r+3100−3844=0
31r2+310r−744=0
To simplify, divide the entire equation by 31:
r2+10r−24=0
Now we need to factor the quadratic:
(r+12)(r−2)=0
Setting each factor to zero gives us:
r+12=0⇒r=−12(not valid since radius cannot be negative)
r−2=0⇒r=2
The radius of the other end of the conical frustum is:
2 m
Topper's Solved these Questions
- CO-ORDINATE GEOMETRY OF TWO DIMENSIONS (CONIC SECTION)Book:MAHAVEER PUBLICATIONChapter:CO-ORDINATE GEOMETRY OF TWO DIMENSIONS (CONIC SECTION)Exercise:QUESTION BANK
Explore 110 Videos
- CONTINUITY OF A FUNCTIONBook:MAHAVEER PUBLICATIONChapter:CONTINUITY OF A FUNCTIONExercise:QUESTION BANK
Explore 21 Videos
Similar Questions
The perimeter of the ends of a frustum are 48 cm and 36 cm. If the height of the frustum is 11 cm, find its volume.
View SolutionA tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m, the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent.
View Solution
Knowledge Check
The volume of a cylinder is 924m3 and its curved surface area is 264m2. The height of the cylinder is:
A4mB5mC6mD7mThe radius of the base of a cylinder is 14 cm and height is 6 cm. The volume of the cylinder is :
A196 πB392 πC1176πDNone of theseHeight and radius of a cylinder are increased by 10%, then the volume of the cylinder, is
A0.331B0.4C0.1D1
A tent has been constructed which is in the form of a right circular cylinder surmounted by a right circular cone whose axis coincides with the axis of the cylinder. If the radius of the base of the cylinder is 50 m, the height of the cylinder is 10 m and the total height of the tent is 15 m, then what is the capacity of the tent in cubic metres ?
View SolutionMayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depr ession at one end . The height of the cylinder is 1.45 m and its radius is 30 cm.
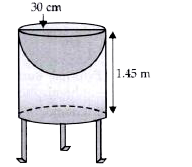
Find the surface area of hemi spherical depression.
View SolutionThe curved surface area of a cylinder is 440m2 and the radius is 5cm. Find its height.
View SolutionThe total surface area of the cylider is 2640m2 and the sum of height and radius of base of cylinder is 30 m. What is the ratio of height and radius of the cylinder ?
View SolutionThe total surface area of the cylider is 2640m2 and the sum of height and radius of base of cylinder is 30 m. What is the ratio of height and radius of the cylinder ?
View Solution

