Express as a prefect square.
To express 1+sinθ as a perfect square, we can follow these steps:
Step 1: Recall the Pythagorean Identity
We know from trigonometry that:
sin2A+cos2A=1
This means we can express 1 in terms of sine and cosine.
Step 2: Rewrite 1
We can rewrite 1 as:
1=sin2θ2+cos2θ2
This is valid because θ2 is just another angle.
Step 3: Express sinθ
Using the double angle formula for sine, we can express sinθ as:
sinθ=2sinθ2cosθ2
Step 4: Combine the Expressions
Now, we can substitute these into our original expression:
1+sinθ=sin2θ2+cos2θ2+2sinθ2cosθ2
Step 5: Recognize the Perfect Square
The expression sin2θ2+cos2θ2+2sinθ2cosθ2 can be recognized as the expansion of a perfect square:
(sinθ2+cosθ2)2
Final Expression
Thus, we can express 1+sinθ as:
1+sinθ=(sinθ2+cosθ2)2
We know from trigonometry that:
sin2A+cos2A=1
This means we can express 1 in terms of sine and cosine.
We can rewrite 1 as:
1=sin2θ2+cos2θ2
This is valid because θ2 is just another angle.
Using the double angle formula for sine, we can express sinθ as:
sinθ=2sinθ2cosθ2
Now, we can substitute these into our original expression:
1+sinθ=sin2θ2+cos2θ2+2sinθ2cosθ2
The expression sin2θ2+cos2θ2+2sinθ2cosθ2 can be recognized as the expansion of a perfect square:
(sinθ2+cosθ2)2
Thus, we can express 1+sinθ as:
1+sinθ=(sinθ2+cosθ2)2
Topper's Solved these Questions
Similar Questions
Knowledge Check
The real value of θ for which the expression 1−isinθ1+2isinθ is purely real is
AnπB(n+1)π/2C(2n+1)π/2DNoneIf the each of algebraic expressions lx2+mx+n,mx2+nx+landnx2+lx+m are prefect squares, then l+mn= _____
A−4B6C−8DNone of these
Express sinθ in terms of cotθ.
View Solution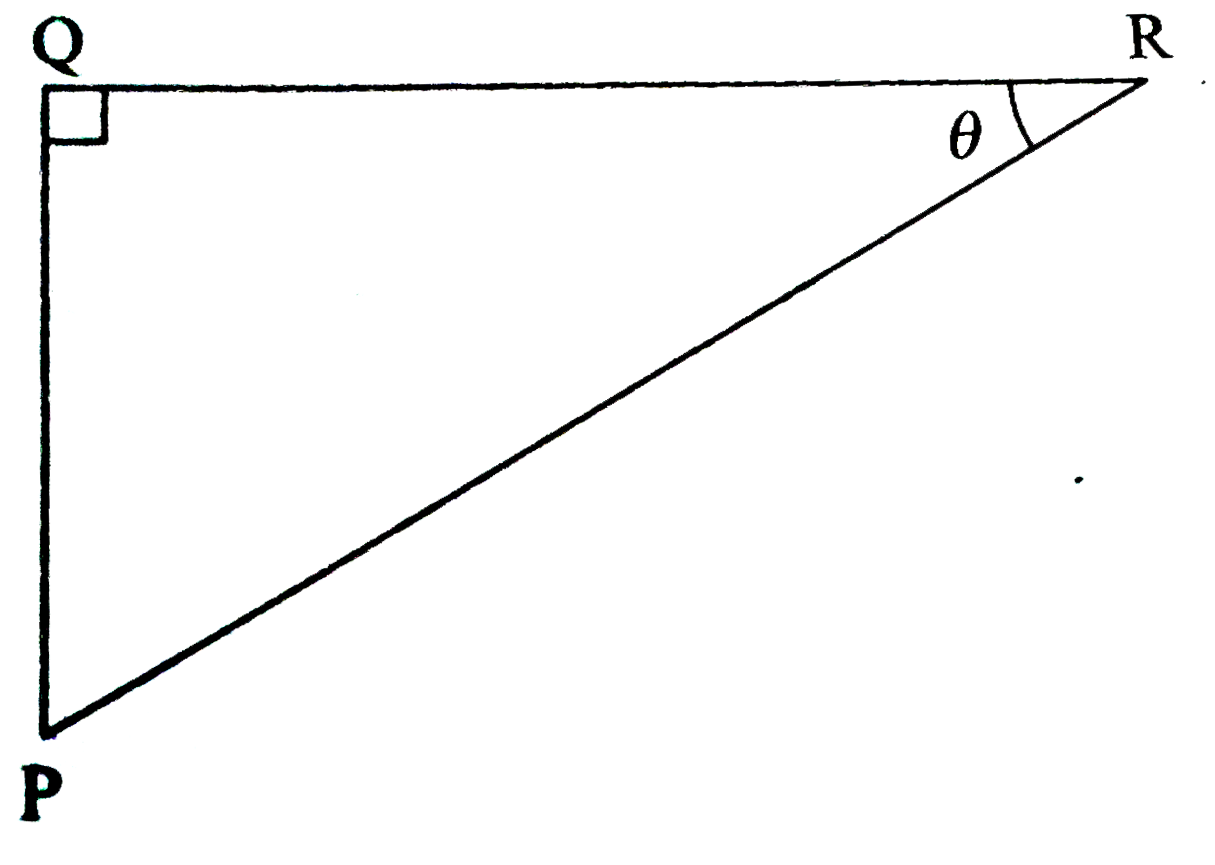
In the figure sinθ=□,tanθ=□
View SolutionExpress sin5θ in terms of sinθ
View SolutionComplete the relation in ratios given below .
(i)sinθcosθ=□
(ii)sinθ=cos(90−□)
(iii)cosθ=sin(90−□)
(iv)tanθ×tan(90−θ)=□
View SolutionFind the sign of the expression sinθ+cosθ when θ=1000
View SolutionExpress 11+cosθ−isinθ in the form of a+ib.
View Solution
