A circle touches the side BC of a ΔABC at P and also touches AB and AC produced at Q and R, respectively. If the perimeter of ΔABC = 26.4 cm, then the length of AQ is:
8.8 cm
13.2 cm
15.4 cm
17.6 cm
The correct Answer is:B
To solve the problem, we need to find the length of AQ given that a circle touches the sides of triangle ABC and the perimeter of the triangle is 26.4 cm.
1. Understanding the Problem:
- The circle touches side BC at point P.
- It also touches the extensions of sides AB and AC at points Q and R, respectively.
- We need to find the length of AQ.
2. Using the Tangent Property:
- From point A, the lengths of the tangents drawn to the circle are equal. Thus:
- AQ=AP (tangent from A to the circle at point Q)
- BP=BQ (tangent from B to the circle at point P)
- CP=CR (tangent from C to the circle at point R)
3. Setting Up the Variables:
- Let AQ=x.
- Then AP=x (since AQ=AP).
- Let BP=y and CP=z.
- Therefore, we can express the sides of the triangle as:
- AB=AQ+BP=x+y
- BC=BP+CP=y+z
- CA=CP+AQ=z+x
4. Writing the Perimeter Equation:
- The perimeter of triangle ABC is given as:
AB+BC+CA=26.4
- Substituting the expressions for the sides:
(x+y)+(y+z)+(z+x)=26.4
- Simplifying this gives:
2x+2y+2z=26.4
- Dividing the entire equation by 2:
x+y+z=13.2
5. Finding AQ:
- Since AQ=x, we can express y and z in terms of x:
y+z=13.2−x
- However, we need to find AQ directly. Since AQ is equal to AP and AP is one of the tangents, we can use the fact that the total of the tangents from point A to the circle is equal to half the perimeter:
AQ=26.42=13.2 cm
6. Final Calculation:
- Since AQ is half of the perimeter, we find that:
AQ=13.2 cm
Conclusion:
The length of AQ is 13.2 cm.
- The circle touches side BC at point P.
- It also touches the extensions of sides AB and AC at points Q and R, respectively.
- We need to find the length of AQ.
- From point A, the lengths of the tangents drawn to the circle are equal. Thus:
- AQ=AP (tangent from A to the circle at point Q)
- BP=BQ (tangent from B to the circle at point P)
- CP=CR (tangent from C to the circle at point R)
- Let AQ=x.
- Then AP=x (since AQ=AP).
- Let BP=y and CP=z.
- Therefore, we can express the sides of the triangle as:
- AB=AQ+BP=x+y
- BC=BP+CP=y+z
- CA=CP+AQ=z+x
- The perimeter of triangle ABC is given as:
AB+BC+CA=26.4
- Substituting the expressions for the sides:
(x+y)+(y+z)+(z+x)=26.4
- Simplifying this gives:
2x+2y+2z=26.4
- Dividing the entire equation by 2:
x+y+z=13.2
- Since AQ=x, we can express y and z in terms of x:
y+z=13.2−x
- However, we need to find AQ directly. Since AQ is equal to AP and AP is one of the tangents, we can use the fact that the total of the tangents from point A to the circle is equal to half the perimeter:
AQ=26.42=13.2 cm
- Since AQ is half of the perimeter, we find that:
AQ=13.2 cm
The length of AQ is 13.2 cm.
Similar Questions
Knowledge Check
In the figure shown here, a circle touches the side BC of a triangle ABC at P and AB and AC produced at Q and R respectively. What is AQ equal to ?
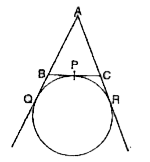 AOne-third of the perimeter of Δ ABC.BHalf of the perimeter of Δ ABC.CTwo-third of the perimeter of Δ ABCDThree-fourth of the perimeter of Δ ABC
AOne-third of the perimeter of Δ ABC.BHalf of the perimeter of Δ ABC.CTwo-third of the perimeter of Δ ABCDThree-fourth of the perimeter of Δ ABCIn figure , the sides AB, BC and CA of triangle ABC, touch a circle at P,Q and R, respectively . If PA = 4 cm , BP = 3 cm and AC = 11 cm , then length of BC is
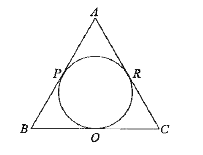 A11 cmB15 cmC14 cmD10 cm
A11 cmB15 cmC14 cmD10 cm
A circle is touching the side BC of ΔABC at P and touching AB and AC produced at Q and R respectively Prove that AQ=12(Perimeter of ΔABC)
View SolutionA circle is touching the side BC of ABC at P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(Perimeter of ABC) .
View SolutionA circle is touching the side BC of a △ABC at point P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(perimeter of △ABC).
View SolutionA circle touches the triangle ΔABC at side BC at point P and touches at Q and R if AB and AC are extended. If perimeter of the triangle is 16 cm then find the length from A to Q.

View SolutionThe side AB, BC and CA of triangle ABC touch a circle at P,Q and R respectively. If PA =4 cm, BP=3 cm and AC=11 cm, then length of BC is

View SolutionThe sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P, Q, and R respectively.
View Solution

