In trapezium ABCD ,AB II DC .The sides AD and BC are produced to meet at E. If AB=15cm,CD=10cm,AD=4cm and BC=5cm, then DE = ?
9 cm
10 cm
6 cm
8 cm
The correct Answer is:4
To solve the problem, we will use the properties of similar triangles. Here is the step-by-step solution:
Step 1: Draw the trapezium
First, we draw trapezium ABCD where AB is parallel to CD. We label the lengths:
- AB = 15 cm
- CD = 10 cm
- AD = 4 cm
- BC = 5 cm
Step 2: Extend the sides AD and BC
Next, we extend the sides AD and BC until they meet at point E.
Step 3: Identify similar triangles
In triangles EAD and EBC, we notice that they share angle E. Since AB is parallel to CD, we can conclude that the angles at point E are equal:
- ∠EAD = ∠EBC (alternate interior angles)
Thus, triangles EAD and EBC are similar by the AA (Angle-Angle) criterion.
Step 4: Set up the proportion based on similarity
From the similarity of triangles, we can set up the following proportion:
ADDE=BCAE
Where:
- AD = 4 cm
- BC = 5 cm
- Let DE = x
- AE = AD + DE = 4 + x
Step 5: Substitute the known values into the proportion
Substituting the known values into the proportion gives us:
4x=54+x
Step 6: Cross-multiply to solve for x
Cross-multiplying gives us:
4(4+x)=5x
Expanding this, we get:
16+4x=5x
Step 7: Rearranging the equation
Rearranging the equation to isolate x:
16=5x−4x
16=x
Step 8: Solve for DE
Thus, we find that:
DE=x=16 cm
Step 9: Verify the solution
We can verify by substituting back into the proportion to ensure both sides are equal.
Final Answer
The length of DE is 8 cm.
---
First, we draw trapezium ABCD where AB is parallel to CD. We label the lengths:
- AB = 15 cm
- CD = 10 cm
- AD = 4 cm
- BC = 5 cm
Next, we extend the sides AD and BC until they meet at point E.
In triangles EAD and EBC, we notice that they share angle E. Since AB is parallel to CD, we can conclude that the angles at point E are equal:
- ∠EAD = ∠EBC (alternate interior angles)
From the similarity of triangles, we can set up the following proportion:
ADDE=BCAE
Where:
- AD = 4 cm
- BC = 5 cm
- Let DE = x
- AE = AD + DE = 4 + x
Substituting the known values into the proportion gives us:
4x=54+x
Cross-multiplying gives us:
4(4+x)=5x
Expanding this, we get:
16+4x=5x
Rearranging the equation to isolate x:
16=5x−4x
16=x
Thus, we find that:
DE=x=16 cm
We can verify by substituting back into the proportion to ensure both sides are equal.
The length of DE is 8 cm.
Topper's Solved these Questions
Similar Questions
In △ABC, D and E are points on the sides AB and AC, respectively, such that DE || BC. If AD = 5cm, DB = 9cm AE =4cm and BC = 15.4cm, then the sum of the length of DE and EC (in cm) is:
△ABC में, D और E क्रमशः AB और AC भुजाओं पर बिंदु इस प्रकार है की DE||BC, यदि AD = 5cm, DB = 9cm AE = 4cm और BC = 15.4cm है, तो DE और EC (सेमी में) की लंबाई का योग है
View SolutionIn the ΔABC, D and E are points on side AB and AC respectively such that DE II BC. If AE=2cm, AD=3cm and BD=4.5cm, then find CE.
View Solution
Knowledge Check
ABCD is a trapezium such that AB and DC are parallel and BC is perpendicular to them. If BC=1 cm, CD=2 cm and ∠ADB=45∘, then the lengths of AB is (in cm)
A125B85C53D163In a trapezium ABCD, AB is a parallel to CD. BD is perpendicular to AD. AC is perpendicular to BC. If AD=BC=15cmandAB=25cm, then the area of the trapezium is :
A192cm2B232cm2C172cm2Dnone of the aboveIn the given figure, ABCD is a trapezium such that AL⊥DCandBM⊥DC. If AB=7cm,BC=AD=5cm and AL=BM=4cm then ar(trap.ABCD)=?
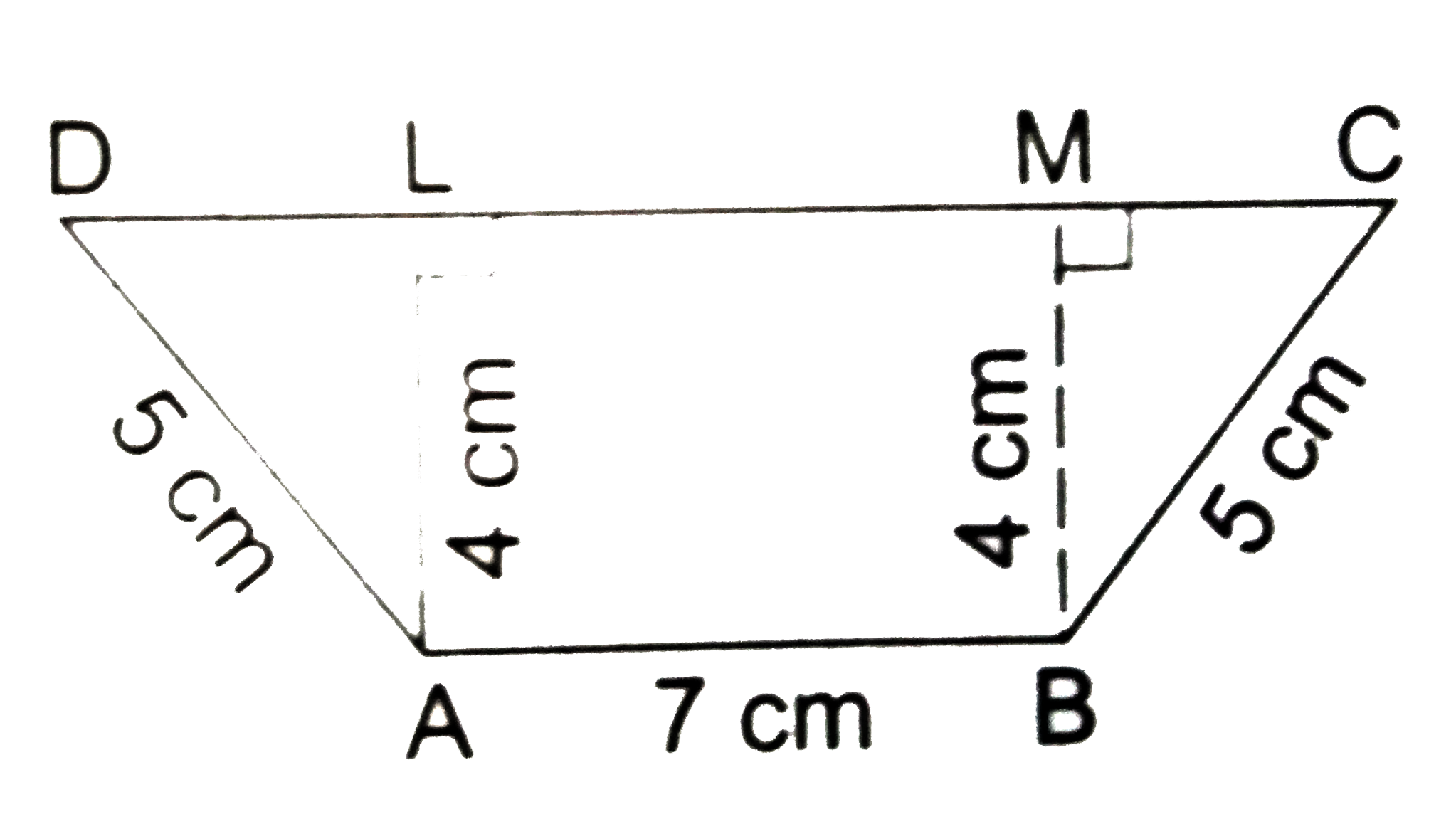 A24cm2B40cm2C55cm2D27.5cm2
A24cm2B40cm2C55cm2D27.5cm2
In a triangle ABC, angle bisector of ∠BAC cut the side BC at D and meet the circumcircle of ΔABC at E. If AC = 4 cm, AD = 5 cm, DE = 3 cm. Find the length of AB.
View SolutionIf D and E are points on the sides AB and AC respectively of DetlaABC such that AB=5.6cm,AD=1.4cm,AC=7.2cmandAE=1.8cm. Show that DE∣∣BC.
View SolutionIn a triangle ABC, angle bisector of ∠BAC cut the side BC at D and meet the circumcircle of ΔABC at E. If AC = 4 cm, AD = 5 cm, DE = 3 cm. Find the length of AB.
View SolutionIn a ΔABC, perpendicular AD from A on BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD=4 cm, then
View SolutionIn ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
View Solution
