Study the following information carefully and answer the given questions: An apple pie of R cm radius has to cut into x identical pieces. Area of top surface of each piece was 0.77cm2 but later on it was found 50% of pie was rotten so the remaining 50% was cut into (x - 3) pieces of area 0.616cm2 each
Find the circumference of the original pie.
445cm
8825cm
17625cm
17650cm
The correct Answer is:D
To solve the problem step by step, we will use the information provided and apply some mathematical reasoning.
Step 1: Calculate the total area of the original apple pie.
The area A of a circle (the top surface of the apple pie) is given by the formula:
A=πr2
Step 2: Set up the equation for the original pie.
The pie is cut into x identical pieces, and the area of each piece is given as 0.77cm2. Therefore, we can express the total area of the pie as:
πr2x=0.77(Equation 1)
Step 3: Calculate the area of the remaining pie after 50% is rotten.
Since 50% of the pie is rotten, the area of the remaining pie is:
πr22
This remaining area is cut into x−3 pieces, with each piece having an area of 0.616cm2. Thus, we can set up the second equation:
πr2/2x−3=0.616(Equation 2)
Step 4: Rearranging Equation 1 and Equation 2.
From Equation 1:
πr2=0.77x(1')
From Equation 2:
πr2=1.232(x−3)(2')
Step 5: Set the equations equal to each other.
Since both expressions equal πr2, we can set them equal:
0.77x=1.232(x−3)
Step 6: Solve for x.
Expanding the right side:
0.77x=1.232x−3.696
Rearranging gives:
1.232x−0.77x=3.696
0.462x=3.696
x=3.6960.462=8
Step 7: Substitute x back into Equation 1 to find r.
Substituting x=8 into Equation 1:
πr2=0.77×8
πr2=6.16
r2=6.16π
Using π≈227:
r2=6.16×722=43.1222≈1.96
Taking the square root:
r≈√1.96≈1.4cm
Step 8: Calculate the circumference of the original pie.
The circumference C of a circle is given by:
C=2πr
Substituting r=1.4:
C=2×227×1.4
Calculating gives:
C=447≈8.8cm
Final Answer:
The circumference of the original pie is 445cm or 8.8cm.
---
The area A of a circle (the top surface of the apple pie) is given by the formula:
A=πr2
The pie is cut into x identical pieces, and the area of each piece is given as 0.77cm2. Therefore, we can express the total area of the pie as:
πr2x=0.77(Equation 1)
Since 50% of the pie is rotten, the area of the remaining pie is:
πr22
This remaining area is cut into x−3 pieces, with each piece having an area of 0.616cm2. Thus, we can set up the second equation:
πr2/2x−3=0.616(Equation 2)
From Equation 1:
πr2=0.77x(1')
From Equation 2:
πr2=1.232(x−3)(2')
Since both expressions equal πr2, we can set them equal:
0.77x=1.232(x−3)
Expanding the right side:
0.77x=1.232x−3.696
Rearranging gives:
1.232x−0.77x=3.696
0.462x=3.696
x=3.6960.462=8
Substituting x=8 into Equation 1:
πr2=0.77×8
πr2=6.16
r2=6.16π
Using π≈227:
r2=6.16×722=43.1222≈1.96
Taking the square root:
r≈√1.96≈1.4cm
The circumference C of a circle is given by:
C=2πr
Substituting r=1.4:
C=2×227×1.4
Calculating gives:
C=447≈8.8cm
The circumference of the original pie is 445cm or 8.8cm.
Similar Questions
Knowledge Check
Study the following information carefully and answer the given questions: An apple pie of R cm radius has to cut into x identical pieces. Area of top surface of each piece was 0.77cm2 but later on it was found 50% of pie was rotten so the remaining 50% was cut into (x - 3) pieces of area 0.616cm2 each
Find the value of X.A10B12C8D6Study the following information carefully and answer the given questions: An apple pie of R cm radius has to cut into x identical pieces. Area of top surface of each piece was 0.77cm2 but later on it was found 50% of pie was rotten so the remaining 50% was cut into (x - 3) pieces of area 0.616cm2 each
If entire pie would have been cut into 11 identical pieces what would have been top surface area of each piece?A0.64cm2B0.56cm2C0.28cm2D0.42cm2Study the following table and answer the questions.

The total number of students scoring 50% or more marks isA1250B875C775D675
Suraj cuts a rope of length 15m 25 cm into 5 equal pieces. What is the length of each piece?
View SolutionStudy the following table and answer the questions.

Which school has the highest number of students scoring exactly 50% marks ?
View SolutionStudy the following Pie-Chart carefully to answer the questions given below.
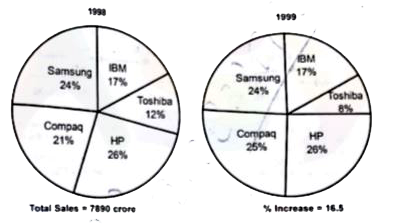
The percentage increase/decrease in the sales of Toshiba in 1999 is approximately-
View SolutionStudy the following table and answer the questions.
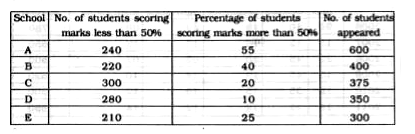
The ratio of the total number of students scoring marks less than 50% to that of scoring marks exactly 50% is
View SolutionSuraj cuts a rope of length 15 m 25 cm into 5 equal pieces. What is the length of each piece?
View Solution