In the following questions 3 series are given. You have to find the value of a, b and c by identifying the pattern of the series and then you have to establish the relation among a, b and c?
I. 1, 601, 721, 751, a, 766
II. 753, 769, b, 765, 763, 764
III. 23, 24, 50, 153, c, 3085
a>b=c
a=b>c
a=b<c
a>b>c
The correct Answer is:B
Pattern of the series I :
1+600=601600+600/5=721 (600/5=120)721+120/4=751 (120/4=30)751+30/3=761 (30/3=10)761+10/5=766 (10/2−5)
So, a = 761
Pattern of the series II :
753+16=769769–8=761761+4=765765–2=763763+1=764
So, b = 761
Pattern of the series III .
23×1+1=2424×2+2=5050×3+3=153153×4+4=616616×5+5=3085
So, C = 616
Hence, a=b>c
Similar Questions
यदि A तथा B दो स्वतंत्र घटनाएँ हों, तो सिद्ध करें कि P(A∪B)=1−P(A')P.(B')
View Solutionसाबित करें कि
sin(B−C)cosBcosC+sin(C−A)cosCcosA+sin(A−B)cosAcosB=0
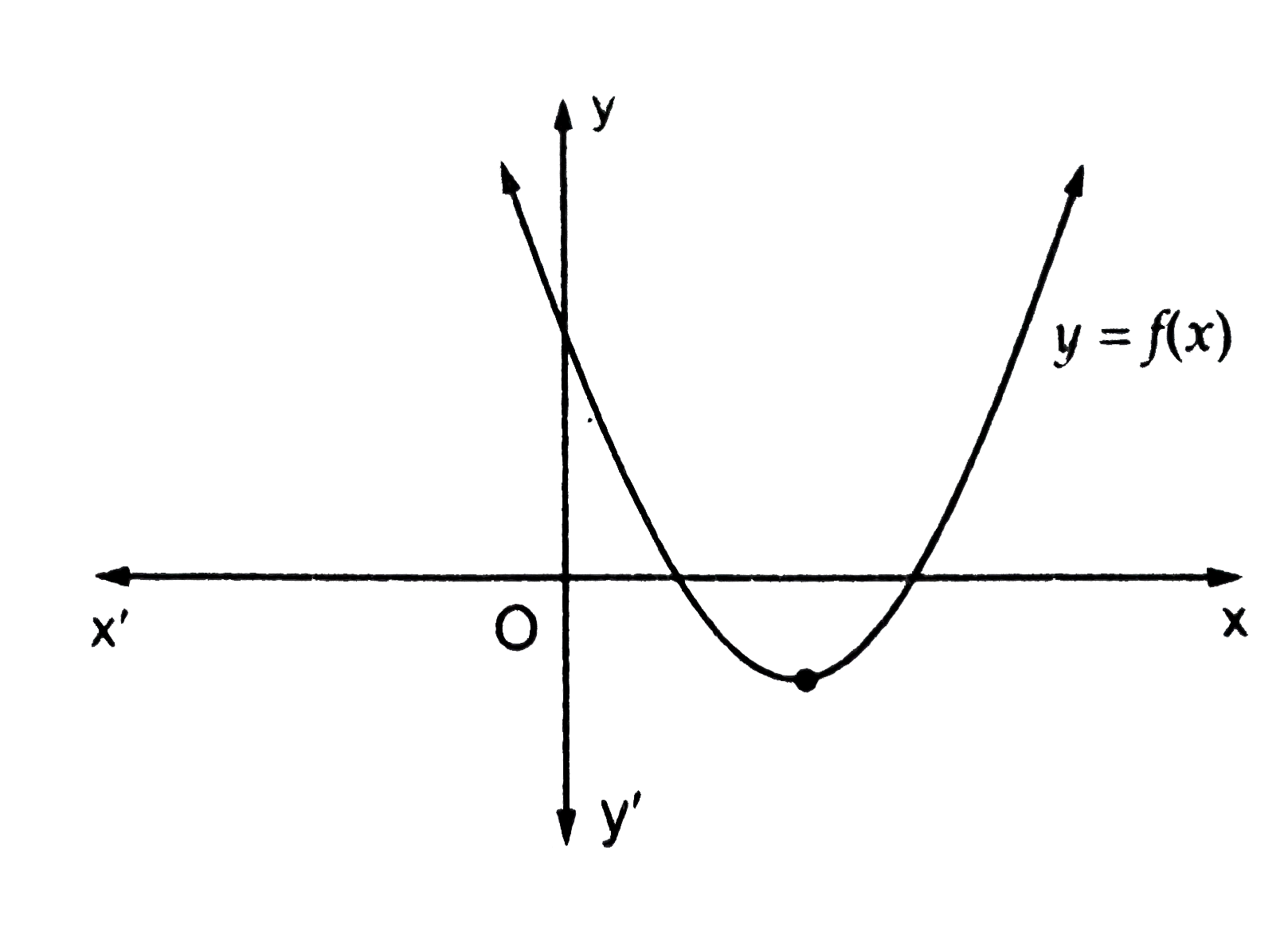
View Solutionबहुपद f(x)=ax2+bx+c का आलेखः चित्र में दर्शाया गया है | 'a' तथा b2−4ac के चिन्ह लिखिए |
View Solutionयदि (secA+tanA)(secB+tanB)(secC+tanC)
=(secA−tanA)(secB−tanB)(secC−tanC) हो, तो सिद्ध करो की प्रत्येक पक्ष ±1के बराबर है।
View Solutionयदि acosθ−bsinθ=c तो, प्रमाणित करो कि
asinθ+bcosθ=±√a2+b2−c2
View Solutionनिम्नलिखित रोगो का संचरण कैसे होता है?
(अ) अमिबता (बी) मलेरिया,
(स) एस्केरिएसिस (द) निमोनिया
(इ) एड्स।
View SolutionIf the function f:{−1,1}→{0,2}, defined by f(x)=ax+b is a surjection, then find a & b.
View SolutionIf ¯a,¯b,¯c are non coplanar vectors, then test for the collinearity of the following points whose position vectors are given.
i) ¯a−2¯b+3¯c,2¯a+3¯b−4¯c,−7¯b+10¯c
ii) 3¯a−4¯b+3¯c,−4¯a+5¯b−6¯c,4¯a−7¯b+6¯c
iii) 2¯a+5¯b−4¯c,¯a+4¯b−3¯c,4¯a+7¯b−6¯c
View Solution