An object is kept at a distance more than twice the focal length (F) from a concave mirror. The distance the image formed will be
less then F
equal to F
between F and 2F
More than 2 F
The correct Answer is:C
To solve the problem of finding the distance at which an image is formed when an object is placed at a distance greater than twice the focal length (2F) from a concave mirror, we can follow these steps:
Step 1: Understand the setup
- We have a concave mirror with a focal length (F).
- The radius of curvature (R) of the mirror is twice the focal length, i.e., R = 2F.
- The object is placed at a distance greater than 2F from the mirror.
Step 2: Use the mirror formula
The mirror formula is given by:
1f=1u+1v
Where:
- f = focal length of the mirror
- u = object distance (taken as negative for concave mirrors)
- v = image distance (to be determined)
Step 3: Assign values
Since the object is placed at a distance greater than 2F, we can say:
u<−2F
For the focal length of a concave mirror, we have:
f=−F
Step 4: Substitute values into the mirror formula
Substituting the values into the mirror formula:
1−F=1u+1v
Rearranging gives:
1v=1−F−1u
Step 5: Analyze the image distance
Since u is a large negative value (greater than -2F), the term 1u will be a small negative number. Thus, 1−F will dominate the equation, indicating that v will be negative, which means the image is formed on the same side as the object.
Step 6: Determine the position of the image
When the object is placed beyond 2F, the image will be formed between F and 2F. This means that the image is real, inverted, and located between the focal point (F) and the center of curvature (2F).
Conclusion
Thus, the distance at which the image is formed is between F and 2F.
- We have a concave mirror with a focal length (F).
- The radius of curvature (R) of the mirror is twice the focal length, i.e., R = 2F.
- The object is placed at a distance greater than 2F from the mirror.
The mirror formula is given by:
1f=1u+1v
Where:
- f = focal length of the mirror
- u = object distance (taken as negative for concave mirrors)
- v = image distance (to be determined)
Since the object is placed at a distance greater than 2F, we can say:
u<−2F
For the focal length of a concave mirror, we have:
f=−F
Substituting the values into the mirror formula:
1−F=1u+1v
Rearranging gives:
1v=1−F−1u
Since u is a large negative value (greater than -2F), the term 1u will be a small negative number. Thus, 1−F will dominate the equation, indicating that v will be negative, which means the image is formed on the same side as the object.
When the object is placed beyond 2F, the image will be formed between F and 2F. This means that the image is real, inverted, and located between the focal point (F) and the center of curvature (2F).
Thus, the distance at which the image is formed is between F and 2F.
Similar Questions
Focal length of the concave lens is 40 cm. An object is kept at a distance 40 cm from the lens. What will be the location and magnification of image formed?
View Solution(a) State the relation between object distance, image distance and focal length of a spherical mirror.
(b) Draw a ray diagram to show the image formed by a concave mirror when an object is placed between pole and focus of the mirror.
(c ) A concave mirror of focal length 15 cm forms an image of an object kept at a distance of 10 cm from the mirror. Find the position, nature and size of the image formed by it.
View Solution
Knowledge Check
An object is placed at a distance of 20 cm from the pole of a concave mirror of focal length 10 cm. The distance of the image formed is
A+20cmB+10CmC−20cmD−10cmFollowing figure illustrates the ray diagram for the formation of image by a concave mirror. The position of the object is beyond the centre of curvature of the concave mirror. On the basis of given diagram .
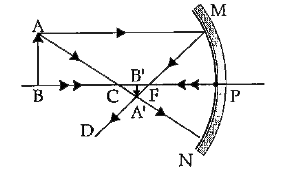
If the focal length of the concave mirror is 10 cm, the image formed will be at a distance ____ABetween 10cm and 15cmBBetween 10cm and 20cmCBeyond 20cmDAt 20cmAn object is kept at a distance 20 cm from a convex mirror of focal length 20 cm. The image will form at
AinfinityBfocusCthe position of objectD10 cm behind the mirror
An object is placed at a distance of 10 cm from a concave mirror. When the distance of object from the mirror is decreased to 6 cm, the image gets 2 times magnified than that in first case. Calculate the focal length of the mirror.
View SolutionIf the distance between the virtual image from Its real object is 60 cm in case of a concave mirror . The focal length of the concave mirror If the image formed is 3 times magnified image is
View SolutionAn object is kept at a distance of 16cm from a thin lens and the image formed is real. If the object is kept at a distance of 6cm from the lens, the image formed is virtual. If the sizes of the images formed are equal, the focal length of the lens will be
View SolutionAn object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View SolutionAn object is placed in front of a convex mirror at a distance equal to the focal length of the mirror. If its focal length is 20 cm, the distance of the image from the mirror is ______ cm
View Solution
