In the following question, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): If the median and mode of a frequency distribution are 150 and 154 respectively. Then its mean is 148.
Reason (R): Mean, median and mode of a frequency distribution are related as 3Mean=3Median - Mode.
Both A and R are true and R is the correct explanation for A.
Both A and R are true and R is not correct explanation for A.
A is true but R is false.
A is false but R is true.
The correct Answer is:A
To solve the problem, we need to analyze the given assertion and reason statements regarding the relationship between mean, median, and mode in a frequency distribution.
1. Understand the Assertion (A):
- The assertion states that if the median is 150 and the mode is 154, then the mean is 148.
2. Understand the Reason (R):
- The reason states that the relationship between mean, median, and mode is given by the formula:
3×Mean=3×Median−Mode
3. Check the Given Formula:
- The correct relationship is:
Mode=3×Median−2×Mean
- However, the reason provided in the question is incorrect.
4. Use the Correct Formula:
- Rearranging the correct formula gives us:
2×Mean=3×Median−Mode
- This can be rewritten as:
Mean=3×Median−Mode2
5. Substitute the Values:
- Substitute the given values of median and mode into the formula:
- Median = 150
- Mode = 154
- Plugging in these values:
Mean=3×150−1542
6. Calculate the Mean:
- Calculate 3×150:
3×150=450
- Now substitute this back into the equation:
Mean=450−1542
- Calculate 450−154:
450−154=296
- Now divide by 2:
Mean=2962=148
7. Conclusion:
- The calculated mean is indeed 148, which confirms the assertion is correct.
- However, the reason provided is incorrect because the formula stated is not the standard relationship between mean, median, and mode.
Final Answer:
- The assertion (A) is true, and the reason (R) is false. Therefore, the correct choice is that the assertion is correct, but the reason is incorrect.
- The assertion states that if the median is 150 and the mode is 154, then the mean is 148.
- The reason states that the relationship between mean, median, and mode is given by the formula:
3×Mean=3×Median−Mode
- The correct relationship is:
Mode=3×Median−2×Mean
- However, the reason provided in the question is incorrect.
- Rearranging the correct formula gives us:
2×Mean=3×Median−Mode
- This can be rewritten as:
Mean=3×Median−Mode2
- Substitute the given values of median and mode into the formula:
- Median = 150
- Mode = 154
- Plugging in these values:
Mean=3×150−1542
- Calculate 3×150:
3×150=450
- Now substitute this back into the equation:
Mean=450−1542
- Calculate 450−154:
450−154=296
- Now divide by 2:
Mean=2962=148
- The calculated mean is indeed 148, which confirms the assertion is correct.
- However, the reason provided is incorrect because the formula stated is not the standard relationship between mean, median, and mode.
- The assertion (A) is true, and the reason (R) is false. Therefore, the correct choice is that the assertion is correct, but the reason is incorrect.
Topper's Solved these Questions
- STATISTICSBook:OSWAL PUBLICATIONChapter:STATISTICSExercise:CASE BASED MCQs
Explore 15 Videos
- STATISTICSBook:OSWAL PUBLICATIONChapter:STATISTICSExercise:Example
Explore 3 Videos
- STATISTICSBook:OSWAL PUBLICATIONChapter:STATISTICSExercise:Assertion and Reasoning Based Questions
Explore 2 Videos
- SOME APPLICATIONS OF TRIGONOMETRY (HEIGHTS AND DISTANCES) Book:OSWAL PUBLICATIONChapter:SOME APPLICATIONS OF TRIGONOMETRY (HEIGHTS AND DISTANCES) Exercise:CASE-BASED MCQs
Explore 15 Videos
- SURFACE AREAS AND VOLUMES Book:OSWAL PUBLICATIONChapter:SURFACE AREAS AND VOLUMES Exercise:BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
Explore 9 Videos
Similar Questions
If the mean and mode of a frequency distribution be 53.4 and 55.2 respectively, find the median
View SolutionIn the following question, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Assertion (A): Mean of given data is 13.81

Reason (R): Mean= ∑FX∑F
View Solution
Knowledge Check
The median and mode of a frequency distribution are 26 and 29 respectively. Then , the mean is
A27.5B24.5C28.4D25.8The mean and mode of a frequency distribution are 28 and 16 respectively .The median is
A22B23.5C24D24.5Mean and median of a simple distribution are 38 and 39 respectively. Then, mode will be
A36B37C41D40
Find the mean and median of the following distribution :
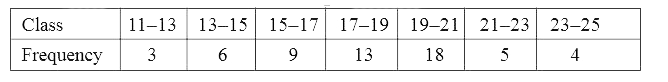
View SolutionFind the median marks for the following frequency distribution :

View SolutionRelation between mean, median and mode -
View SolutionIf in a frequency distribution, the mean and median are 21 and 22 respectively, then its mode is approximately
View SolutionIf the mean and median of a set of numbers are 8.2 and 8.4, respectively, then mode is
View Solution

