The focus of the parabola
To find the focus of the parabola given by the equation y2−8x−2y+2=0, we will convert this equation into the standard form of a parabola and then use that to find the coordinates of the focus.
Step 1: Write the given equation.
We start with the equation:
y2−8x−2y+2=0
Step 2: Rearrange the equation.
We can rearrange the equation to group the y terms together:
y2−2y−8x+2=0
Step 3: Complete the square for the y terms.
To complete the square for the y terms, we take the coefficient of y (which is -2), halve it to get -1, and then square it to get 1. We add and subtract 1:
(y2−2y+1)−1−8x+2=0
This simplifies to:
(y−1)2−8x+1=0
Step 4: Move the other terms to the right side.
Now, we can move the terms involving x to the right side:
(y−1)2=8x−1
Step 5: Rewrite the equation.
We can rewrite this as:
(y−1)2=8(x−18)
Step 6: Identify the standard form.
This is now in the standard form of a parabola:
(y−k)2=4p(x−h)
where k=1, h=18, and 4p=8 which gives p=2.
Step 7: Find the coordinates of the focus.
The coordinates of the focus can be found using the formula:
(h+p,k)
Substituting the values we found:
(18+2,1)
Calculating 18+2:
18+168=178
Thus, the coordinates of the focus are:
(178,1)
Final Answer:
The focus of the parabola is (178,1).
---
We start with the equation:
y2−8x−2y+2=0
We can rearrange the equation to group the y terms together:
y2−2y−8x+2=0
To complete the square for the y terms, we take the coefficient of y (which is -2), halve it to get -1, and then square it to get 1. We add and subtract 1:
(y2−2y+1)−1−8x+2=0
This simplifies to:
(y−1)2−8x+1=0
Now, we can move the terms involving x to the right side:
(y−1)2=8x−1
We can rewrite this as:
(y−1)2=8(x−18)
This is now in the standard form of a parabola:
(y−k)2=4p(x−h)
where k=1, h=18, and 4p=8 which gives p=2.
The coordinates of the focus can be found using the formula:
(h+p,k)
Substituting the values we found:
(18+2,1)
Calculating 18+2:
18+168=178
Thus, the coordinates of the focus are:
(178,1)
The focus of the parabola is (178,1).
Topper's Solved these Questions
Similar Questions
Knowledge Check
The mirror image of the focus to the parabola 4(x+y)=y2 w.r.t. the directrix is
A(0, 2)B(2, 2)C(-4, 2)D(-2, 2)In the adjacent figure a parabola is drawn to pass through the vertices B,C and D of the square ABCD. If A(2,1),C(2,3), then focus of this parabola is
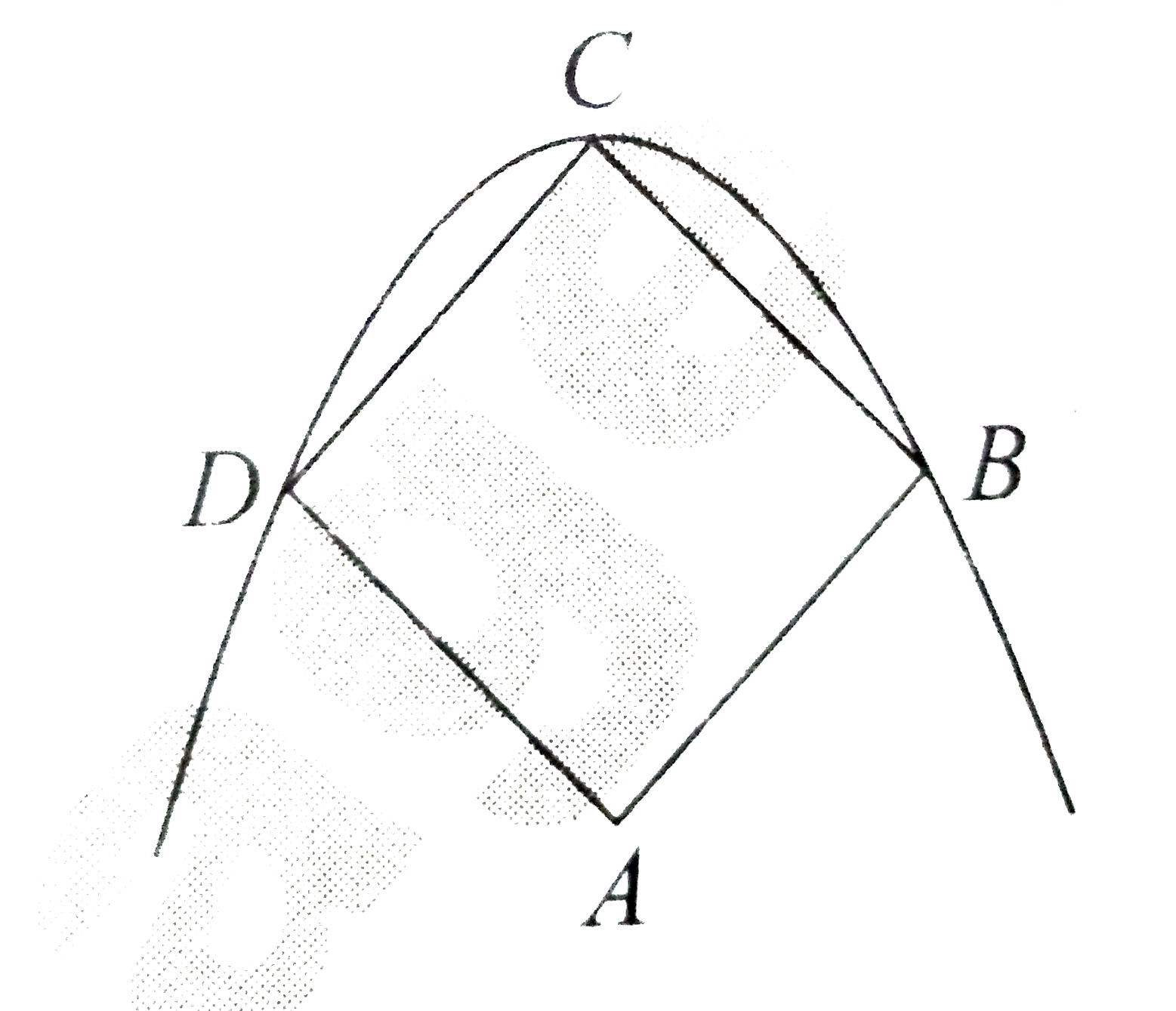 A(1,114)B(2,114)C(3,134)D(2,134)
A(1,114)B(2,114)C(3,134)D(2,134)If the focus of a parabola is at (0,-3) and its directrix is y = 3, then its equation is
Ax2=−12yBx2=12yCy2=−12xDy2=112x
The focus of a parabola is (1,2) and the point of intersection of the directrix and axis is (2,3).Then the equation of the parabola is
View SolutionWrite the distance between the vertex and focus of the parabola y2+6y+2x+5=0.
View SolutionThe vertex and focus of the, parabola 2y^(2)+5x-6y+1=0 are respectively.
View SolutionFind the point on the parabola y2=4ax(a>0) which forms a triangle of area 3a2 with the vertex and focus of the parabola.
View SolutionIf the focus of a parabola is (0,−3) and its directrix is y=3, then its equation is
View Solution

