The given figure in the questions has five squares and four equilateral triangles. Two squares and two triangles are shaded. The figure is folded along the dividing lines,the squares by 90∘ and triangles by 45∘so as to form a closed three dimensional object . The object is then placed with its apex pointing towards your left . Which one among the figures given in the alternatives can be seen ?
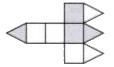




The correct Answer is:A
Step by step video & image solution for The given figure in the questions has five squares and four equilateral triangles. Two squares and two triangles are shaded. The figure is folded along the dividing lines,the squares by 90^(@) and triangles by 45^(@)so as to form a closed three dimensional object . The object is then placed with its apex pointing towards your left . Which one among the figures given in the alternatives can be seen ? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
Similar Practice Problems
- Question 1 - Select One
The side of the square is 6 cm. Two equilateral triangles are drawn as shown here. Find the perimeter of the figure.
 A60 cmB36 cmC42 cmD48 cm
A60 cmB36 cmC42 cmD48 cm - Question 1 - Select One
An equilateral triangle is drawn on the diagonal of a square. The ratio of the area of the triangle to that of the square is
A√3:2B√2:√3C2:√3D1:√2 - Question 1 - Select One
Find the number of squares and triangles in the given figure.
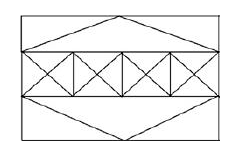 A38 Triangles, 7 SquaresB44 Triangles, 7 SquaresC40 Triangles, 8 SquaresD36 Triangles, 8 Squares
A38 Triangles, 7 SquaresB44 Triangles, 7 SquaresC40 Triangles, 8 SquaresD36 Triangles, 8 Squares
Similar Questions
The given figure shows a square ABCD and an equilateral triangle ABP Calculate
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP Calculate:
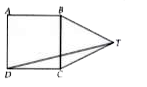
View SolutionIn the given figure, ABCD is a square and ΔBCT is an equilateral triangle. Find ∠BTD.
 View Solution
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate: ∠AOB,∠BPC
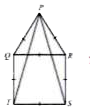
View SolutionIn the given figure, PQR is an equilateral triangle and QRST is a square. Then ∠PSR=
 View Solution
View SolutionIn the given figure equilateral triangle EDC surmounts the square ABCD. α=
View SolutionIn the given figure ABCD is a square with side 15 and BCE is an equilateral triangle. The ratio of the shaded region to the unshaded region is :
View Solution

