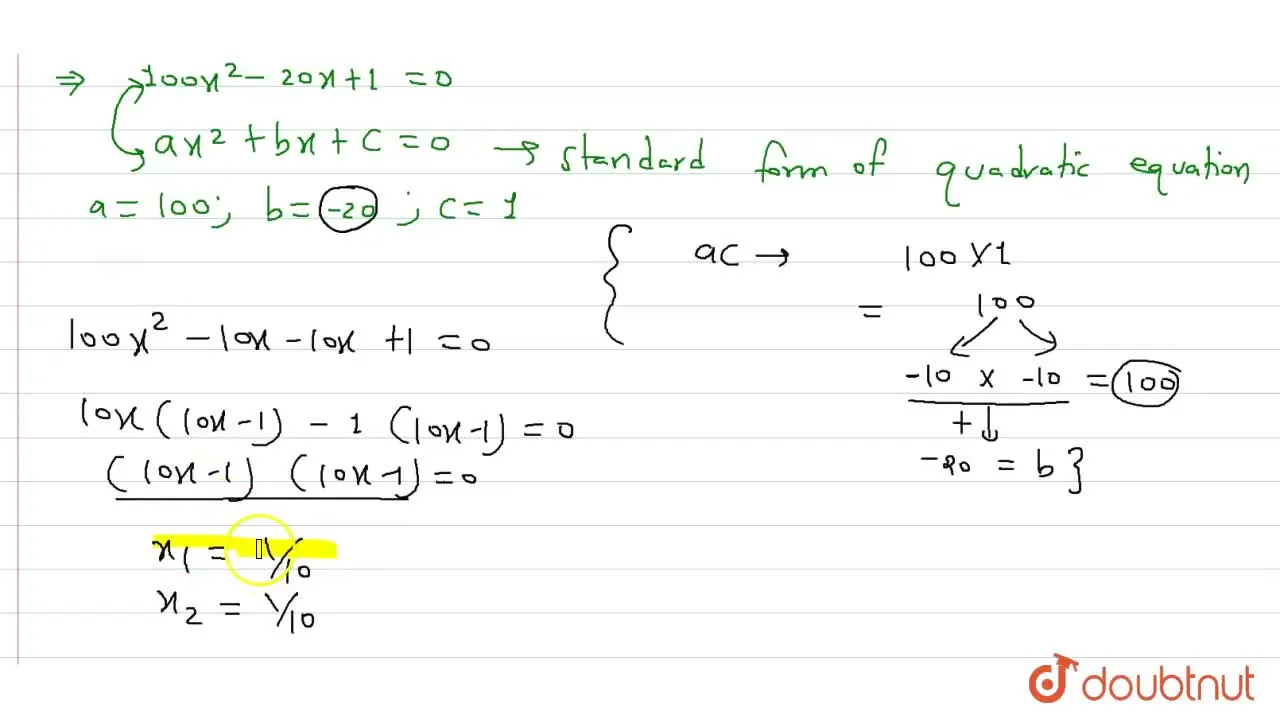Find the roots of the following quadratic equations by factorisation :
100x2−20x+1=0
Step by step video & image solution for Find the roots of the following quadratic equations by factorisation : 100x^(2)-20x+1=0 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
- BOOK - OSWAL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - NCERT CORNER (Exercise- 4.3)18videos
QUADRATIC EQUATIONS
- BOOK - OSWAL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - NCERT CORNER (Exercise- 4.4)8videos
QUADRATIC EQUATIONS
- BOOK - OSWAL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - NCERT CORNER (Exercise- 4.1)12videos
QUADRATIC EQUATIONS
- BOOK - OSWAL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Self Assessment66videos
PROBABILITY
- BOOK - OSWAL PUBLICATIONCHAPTER - REAL NUMBERSEXERCISE - Self-Assessment11videos
REAL NUMBERS
Similar Questions
Find the roots of the following Quadratic Equations by factrorization .
100x2−20x+1=0View SolutionFind the roots of the following quadratic equations by factorisation :
2x2+x−6=0View SolutionFind the roots of the following quadratic equations by factorisation :
x2−3x−10=0View SolutionFind the roots of the following quadratic equations by factorisation :
2x2−x+18=0View SolutionFind the roots of the following quadratic equations by factorisation :
(i) x2−3x−10=0 (ii) 2x2+x−6=0 (iii) √2x2+7x+5√2=0
(iv) 2x2−x+18=0 (v) 100x2−20x+1=0 (vi) 2x2+az−a2=0View SolutionFind the roots of the following quadratic equations by factorisation:
(i) x2−3x−10=0
(ii) 2x2−x−6=0
(iii) √2x2+7x+5√2=0
(iv) 100x2−20x+1=0
(v) 100x2−20x+1=0View SolutionFind the roots of the following Quadratic Equations by factrorization .
2x2+x−6=0View SolutionFind the roots of the following quadratic equations by the factorisation method.
21x2−2x+121=0View SolutionFind the roots of the following Quadratic Equations by factrorization .
x2−3x−10=0View SolutionFind the roots of the following quadratic equations by factorisation :
√2x2+7x+5√2=0View Solution