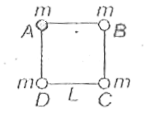
Three particles A, B, and C each having mass m are kept along a straight line with AB = BC = l. A fourth particle D is kept on the perpendicular bisecter of AC at a distance l from B. Determine the gravitational force on D.Solution in Marathi
CD=AD=√AB2+BD2=√2l
Gravitational force on D = Vector sum of gravitational forces due to A, B and C.

Force due to A=Gmm(AD)2=Gm22l2. This will be along ¯¯¯¯¯¯DA
Force due to C=Gmm(CD)2=Gm22l2. This is along ¯¯¯¯¯¯DC
Force due to B=Gmm(BD)2=Gm2l2. This is along ¯¯¯¯¯¯DB
We can resolve the forces along horizontal and vertical directions.
Let the unit vector along horizontal direction¯¯¯¯¯¯AC be hati and the vertical direction ¯¯¯¯¯¯BD be ˆj
Net horizontal force on D
=Gm22l2cos45∘(−ˆi)+Gm2l2cos90∘(ˆi)+Gm22l2cos45∘(ˆi)
=−Gm22√2l2+Gm22√2l2=0
Net vertical force on D
=Gm22l2cos45∘(−ˆj)+Gm2l2(−ˆj)+Gm22l2cos45∘(−ˆj)
=−Gm2l2(1√2+1)(ˆj)
=Gm2l2(1√2+1)(−ˆj)
(−ˆj) shows that the net force is directed along DB.
Similar Questions
Three particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View SolutionTwo charged particles each having a charge +q and mass m are kept at a distance d. if they are in equilibrium under the gravitational force and the electric force between them, then the ratio qm or specific charge of each particle is
View SolutionFour particles A,B, C and D each of mass m are kept at the corners of a square of side L. Now the particle D is taken to infinity by an external agent keeping the other particles fixed at their respective positions . The work done by the gravitational force acting on the particle D During its movement is
View SolutionThree particles of the same mass are kept at the vertices of an equilateral triangle. The mass of each particle is m and the length of an arm of the triangle is l. Due to the the mutual gravitational force of attraction, the particles revolve along the circumcircle of the triangle. Find the velocity of each particle.
View SolutionTwo particles of masses m_1 and m_2 are kept at a separation of d. when a third particle is kept at a distance of d/3 from m_1 , then it does not experience any net force. Determine the ratio (m_2)/(m_1) .
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View SolutionTwo particles A and B , each carrying charge Q are held fixed with a separation D between them. A particle C having mass m and charge q is kept at the middle point of the line AB. If particle C is displaced through a distance x along the line AB. What will be the time period of the oscillations.
View SolutionThree points A , B and C each of mass m is placed in a line with AB=BC=d. Find the gravitational force on a fourth particle P of the same mass placed at a distance d from particle B on the perpendicular bisector of the line AC.
View Solution

