Question

$\mu =1.5$ के पदार्थ से बनी एक छोटी पारदर्शी सिल्ली (स्लेब) $A{S}_2$ के अनुदिश रखी है (चित्र)| O से अब प्राप्त मुख्य उच्चिष्पा तथा काँच की पट्टिका की अनुपस्थिति में प्राप्त मुख्य उच्चिष्ठ के किसी भी ओर प्रथम निम्निष्ठ की दूरी क्या होगी।?

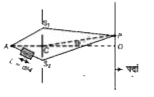
$AC+CO+D,S_{1}C=S_{2}C=d<<D$

Options

A. बिन्दु O के ऊपर `(2D)/(sqrt(247))` और बिन्दु O के नीचे `(5)/(sqrt(231))`
B. विन्दु O के ऊपर `3sqrt(247)` और बिन्दु O के नीचे `5 sqrt(231)`
C. बिन्दु O से नीचे `(5)/(sqrt(465))` और बिन्दु O के नीचे `(3D)/(sqrt(247))`
D. उपरोक्त में से कोई नहीं

Answer

A

Explanation

यदि पारदर्शी काँच पट्टिका का अपवर्तनांक `mu` है, तब पथान्तर `=2d sin theta + (mu-1) L`
झिरों की चौड़ाई = 2d
मुख्य उच्चिष्ठ के लिए (पथान्तर शून्य है)
अर्थात्  `2d sin theta_(0)+(mu-1)L=0" या "sin theta_(0) =-(L(mu-1))/(2d)=(-L(0.5))/(2d)`
`[because L=d//4]`
 या `sin theta_(0)=(-1)/(16)`
`OP=D tan theta_(0)=D sin theta_(0)=(-D)/(16)`
प्रथम उच्चिष्ठ के लिए,पथान्तर `pm (lamda)/(2)` है।
`2d sin theta_(1)+0.5L = pm (lamda)/(2)` या `sin theta_(1)=(pm (lamda)/(2)-0.5L)/(2d)`
`=(pm lamda//2-d//8)/(2 d)`
`=(pm lamda//2-2lamda//8)/(2 lamda)`
`= pm (1)/(4)-(1)/(16)`
[`because` जब तरंग की तरंगदैर्ध्य का मान, झिरों की चौड़ाई के तुल्य होता है, तो विवर्तन होता है।]
धनात्मक भाग पर, `sin theta_(1)= +(1)/(4)-(1)/(16)=(3)/(16)`
ऋणात्मक भाग पर,
`sin theta_(1).. =-(1)/(4)-(1)/(16)=-(5)/(16)`
धनात्मक भाग पर प्रथम मुख्य उच्चिष्ठ की दूरी,
`D tan theta_(1).=D (sin theta_(1))/(sqrt(1-sin^(2)theta_(1))`
`=D(3)/(sqrt(16^(2)-3^(2))`
`=(3D)/(sqrt(247))`, बिन्दु O के ऊपर
ऋणात्मक भाग में प्रथम मुख्य निम्निष्ठ की दूरी,
`D tan theta_(1)..=(5)/(sqrt(16^(2)-5^(2)))=(5)/(sqrt(231))` , बिन्दु O के नीचे।