चित्र में दर्शाए गए अनुसार चार समरूप एकवर्णी स्रोत A, B,C, D समान तरंगदैर्ध्य λ की तरंगें उत्पन्न करते हैं तथा कला-सम्बन्ध हैं (चित्र)। B से समान दूरी पर दो अभिग्राही R1तथा R2 हैं और यह दूरी बहुत अधिक है।
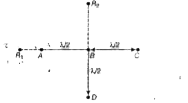
निम्न में से कौन-सा अभिग्राही अधिक सिग्नल लेता है?
R1
R2
R1तथाR2
इनमें से कोई नहीं
The correct Answer is:B
किसी एक बिन्दु पर परिणामी विक्षोभ की गणना व्यक्तिगत स्रोतों के कारण विक्षोभों के योग से की जाएगी।
मान लीजिए ग्राही (receiver) R1 पर विक्षोभ है, जोकि B से d दूरी पर है।
माना R1 पर A के कारण तरंग,
YA=acosωt है। सिग्नल A से B का पथान्तर λ2 है एवं इसलिए कलान्तर π है।
अत: R1 से B के कारण तरंग,
YB=acos(ωt−π)=−acosωt
सिग्नल C से A का पथान्तर, λ है एवं इसलिए कलान्तर 2π है।
अत: R1 से C के कारण तरंग,
acos(ωt−2π)
=acosωt
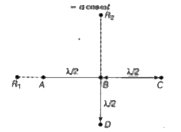
सिग्नल D से A के मध्य पथान्तर है,
√d2+(λ2)2−(d−λ/2)
=d(1+λ4d2)1/2−d+λ2
=d(1+λ28d2)1/2−d+λ2≈λ2
(∵d>>λ)
अत: कलान्तर π है ।
∵YD=acos(ωt−π)=−acosωt
इस प्रकार चारों स्त्रोतो से, R1 पर प्राप्त सिग्नल,
YR1=yA+yB+yC+yD
=acosωt−acosωt+acosωt−acosωt=0 तथा B स्त्रोत से R2 पर प्राप्त सिग्नल
yB=a1cosωt
D तक B पर उपस्थित सिग्नलों के बीच पथान्तर
λ2 है।
yD=−a1cosωt
A तथा B पर उपस्थित सिग्नलों के बीच सिग्नल
√d2+(λ2)2−d=d(1+λ4d2)1/2−d≅λ8d2
d>>λ, तब पथान्तर →0 तथा कलान्तर =2πλ(18λ28d2)→0
yA=a1cos(ωt−ϕ)
yC=a1cos(ωt−ϕ)
R2 के द्वारा प्राप्त सिग्नल
yA+yB+yC+yD=2a1cos(ωt−ϕ)
|y|2=4a21cos2(ωt−ϕ)
∴<I>=2a21
इस प्रकार R1 पर अधिक आयाम का सिग्नल प्राप्त होता है।
Similar Questions
इस प्रश्न में, चार शब्द दिए गए हैं, जिनमें से तीन किसी तरह से समान हैं और चौथा एक अलग है। विषम को चुनें?
View SolutionA is 25% more than B while B is 20% less than C and C is 10% more than D. Which of the following is not true?
A,B से 25% अधिक है जबकि B, C से 20% कम है और C, D से 10% अधिक हे | निम्न में से कौन सा सही नहीं है ?
View Solutionनिम्न में से किस पत्रिका का सम्बन्ध इलाहाबाद से हैं ?
View Solutionनिम्नलिखित में से कौन-सा, कनाडा, चिली तथा जर्मनी के समान है?
View Solution(-1-1) और (4, 2) से समान दूरी पर स्थित बिन्दुओं के बिन्दुपथ का समीकरण है
View Solutionनिम्नलिखित में से कौन से हाइड्रॉक्साइड Al(OH_(2)) की तुलना में अधिक क्षारीय नहीं है ?
View Solutionनिम्न में से कितने कार्बधनायन प्राथमिक एलिल कार्बधनायन की तुलना में अधिक स्थायी होते हैं?

View Solutionनिम्नलिखित में से कौन सा / से कथन सत्य है/हैं: बोरैजीन ऐरोमैटिक है चार समस्थानिक द्विप्रतिस्थापित बोरैजीन अणु B_3N_3H_4X_4 है बोरैजीन, बेन्जीन की तुलना में योजन अभिक्रियाओं के प्रति अधिक अभिक्रियाशील है B_2H_6 में कदली आबंध लंबे लेकिन सामान्य B-H आबंध से अधिक प्रबल होते हैं
View Solution
