2λ दूरी पर स्थित दो कला-सम्बद्ध स्रोत S1 व S2 समान कला में कम्पित होकर तरंगदैर्ध्य λ का प्रकाश उत्सर्जित करते हैं। S2 से जाने वाली व S1S2 के लम्बवत् रेखा पर S2 से कितनी दूरी पर हैं, न्यूनतम तीव्रता उत्पन्न होती है?
7λ12
15λ4
λ2
3λ2
The correct Answer is:A
दिया गया है,
S1 और S2 स्रोतों के मध्य दूरी =2λ
बिन्दु P पर निम्नतम तीव्रता के लिए, बिन्दु P पर विषमपोषी व्यतिकरण होगा।
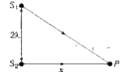
अत: S1P−S2P=Δx (पथान्तर)
=(2n+1)λ2 (विषमपोषी व्यतिकरण के लिए)
निम्नतम दूरी के लिए,
S1P−S2P=3λ2≠λ2....(i)
⇒√x2+(2λ)2−x=3λ2
⇒x2+(2λ)2=[x+(3λ2)]2
⇒x2+4λ2=x2+9λ24+2x.3λ2
⇒x⋅3λ=4λ2−9λ24=7λ24⇒x=7λ12
नोट यदि समी (i) द्वारा S1P=S2P=λ2 है, तो x=15λ4 जोकि 7λ12 से ज्यादा है।
Similar Questions
Let S1,S2,......S101 be consecutive terms of A.P. If 1S1S2+1S2S3+......+1S100S101=16 and S1+S101=50, then |S1−S101| is equal to
View SolutionIf s_(r)=alpha^(r)+beta^(r)+gamma^(r) Then |(s_(0),s_(1),s_(2)),(s_(1),s_(2),s_(3)),(s_(2),s_(3),s_(4))| Value of
View SolutionIf s_(r)=alpha^(r)+beta^(r)+gamma^(r) Then |(s_(0),s_(1),s_(2)),(s_(1),s_(2),s_(3)),(s_(2),s_(3),s_(4))| Value of
View SolutionIf S1,S2andS3 be respectively the sum of n, 2n and 3n terms of a G.P. Prove that S1(S3−S2)=(S2−S1)2.
View SolutionIf S1,S2,S3be respectively the sum of n, 2n and 3n terms of a GP, then S1(S3−S2)(S2−S1)2 is equal to
View SolutionIf S1,S2,S3be respectively the sum of n, 2n and 3n terms of a GP, then S1(S3−S2)(S2−S1)2 is equal to
View Solution(-1-1) और (4, 2) से समान दूरी पर स्थित बिन्दुओं के बिन्दुपथ का समीकरण है
View SolutionIf S_(1), S_(2) , and S_(3) are, respectively, the sum of n, 2n and 3n terms of a G.P., then (S_(1)(S_(3)-S_(2)))/((S_(2)-S_(1)^(2)) is equal to
View Solution