Question

$m_1$ तथा $m_2$ दो द्रव्यमान, निर्देश निकाय में स्थित हैं, जैसाकि चित्र में दिखाया गया है

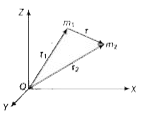
माना F, बिन्दु द्रव्यमान $m_2$ पर दूसरे बिन्दु द्रव्यमान $m_1$ के कारण लगने वाला बल है।
किसी बिन्दु द्रव्यमान $m_1$ के कारण $m_2$ पर लगने वाले बल का परिमाण $F_2$ है

Options

A. `|F|=(Gm_(1)m_(2))/(r^(3))`
B. `|F|=(Gm_(1)m_(2))/(r^(2))`
C. `|F|=(Gm_(1)m_(2))/(r)`
D. `|F|=(Gm_(1)m_(2))/(r^(1//2))`

Answer

B

Explanation

न्यूटन के गुरुत्वाकर्षण नियम के अनुसार,
`|F|=(Gm_(1)m_(2))/(|r|^(2))=(Gm_(1)m_(2))/(r^(2))[:.|r|=r]`