Find by integration the volume of the solid generated by revolving about the y axis the region enclosed by x2=1+yandy=3
The correct Answer is:8π
Topper's Solved these Questions
- APPLICATIONS OF INTEGRATION Book:NCERT TAMILChapter:APPLICATIONS OF INTEGRATION Exercise:EXERCISE 9.10
Explore 20 Videos
- APPLICATIONS OF INTEGRATION Book:NCERT TAMILChapter:APPLICATIONS OF INTEGRATION Exercise:EXERCISE 9.8
Explore 5 Videos
- APPLICATIONS OF DIFFERENTIAL CALCULUSBook:NCERT TAMILChapter:APPLICATIONS OF DIFFERENTIAL CALCULUSExercise:Exercise 7.10
Explore 20 Videos
- APPLICATIONS OF MATRICES AND DETERMINANTSBook:NCERT TAMILChapter:APPLICATIONS OF MATRICES AND DETERMINANTSExercise:EXERCISE 1.8
Explore 25 Videos
Similar Questions
Knowledge Check
The volume of solid generated by revolving about the y-axis the figure bounded by the parabola y=x2andx=y2 is
A215πB245πC215πD524πThe volume of the solid obtained by revolving about y-axis the area enclosed between the ellipse x2+9y2=9 and the strangth line x+3y=3, in the first quadrant is
A3πB4πC6πD9π
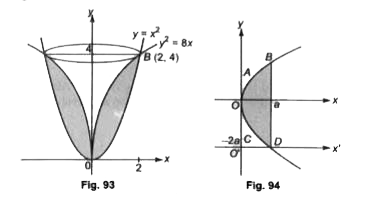
Find the volume of the solid generated by revolving about the line y=−2a the figure bounded by the parabola y2=4ax and the straight line x=a
View SolutionFind the volume of the solid generated by revolving about the x-axis the figure bounded by the straight lines y=x+1,y=2x+1andx=2.
View SolutionCompute the volume of the solid generated by revolving about the x-axis the figure bounded by the parabola y=0.25x2+2 and the straight line 5x−8y+14=0
View SolutionCompute the volume of the solid generated by revolving about the x-axis the area bounded by the axes of coordinates and the parabola x12+y12=a12.
View SolutionFind the volume of the solid generated by revolving, about the x-axis, the infinite branch of the curve y=2(1x−1x2)forx≥1.
View SolutionGiven: the cycloid x=a(t−sint),y=a(1−cost),0≤t≤2π
Compute. (a) the areas of the surface formed by revolving the arc OBA about the x and y-axis,
(b) the volumes of the solids generated by revolving the figure OBAO about the y-axis and the axis BC,
(c ) the area of the surface generated by revolving the are BA about the axis BC,
(d) the volume of the solid generated by revolving the figure ODBEABO about the tangent line DE touching the figure at the vertex B,
(e ) the area of the surface formed by revolving the are of the cycloid (see item (d)]
View Solution

