समान दाब पर ρ1 और ρ2 घनत्व की दो एक परमाणुक गैसो में ध्वनि के वेग क्रमशः v1 और v2 है। यदि ρ1ρ2=4 तब v1v2 का मान है -
14
12
2
4
The correct Answer is:B
Step by step video, text & image solution for समान दाब पर rho_(1) और rho_(2) घनत्व की दो एक परमाणुक गैसो में ध्वनि के वेग क्रमशः v_(1) और v_(2) है। यदि rho_(1)/rho_(2)=4 तब v_(1)/v_(2) का मान है - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The velocities of sound at the same temperature in two monoatomic gases of densities rho_(2) and rho_(2) are v_(1) and v_(2) respectively. If rho_(2)//rho_(2) = 4 , then value of v_(1)//v_(2) is :
View SolutionDensity in two atomic gases at the same pressure rho_(1) And rho_(2) But the sound wave velocity respectively v_(1) And v_(2) is. (rho_(1))/(rho_(2))=4 so (v_(1))/(v_(2)) Will happen -
View Solutionv_(1) and v_(2) are the velocities of sound at the same temperature in two monoatomic gases of densities rho_(1) and rho_(2) respectively. If (rho_(1))/(rho_(2))=(1)/(4) then the ratio of velocities v_(1) and v_(2) is
View SolutionA body of density p floats with a volume V_(s) of its total volume V immersed in one liquid of density rho_(1) and with the remainder of volume V_(2) immersed in another liquid of density rho where. rho_(1) gt rho_(2) find V_(1) and V_(2)
View SolutionThe ratio of accelerations due to gravity g1:g2 on the surface of two planets is 5:2 and the ratio of their respective average densities ρ1:ρ2 is 2:1. What is the ratio of respective escape velocities v1:v2 from the surface of the planets ?
View SolutionA body of density ρ floats with volume V1 of its total volume V immersed in a liquid of density ρ1 and with the remainder of volume V2 immersed in another liquid of density ρ2 where ρ1>ρ2. Find the volume immersed in two liquids. (V1 and V2).
View SolutionThe light cone is in equilibrium under the action of hydrostatic forces of two liquids of densities ρ1 and ρ2. Find ρ1/ρ2. Find ρ1 and ρ2.
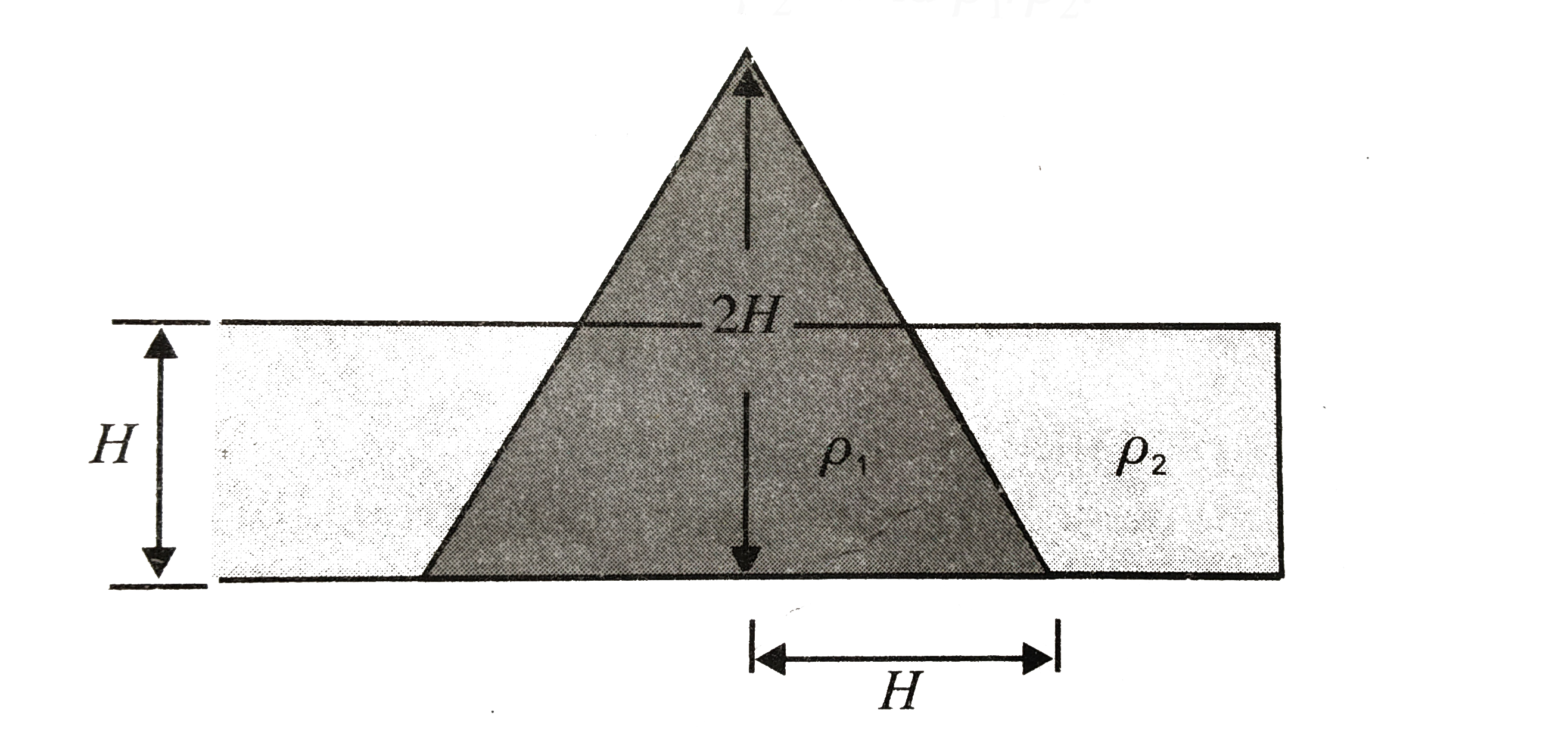
View SolutionStatement I: When a body floats such that its parts are immersed into two immiscible liquids, then force exerted by liquid 1 is of magnitude rho_(1)v_(1)g . Statement II: Total buoyant force =rho_(1)v_(1)g+rho_(2)v_(2)g .
View Solution
