In each of the following questions, a series of number / alphabet is given which follow certain rules. One of the number / alphabet is missing. Choose the missing number / alphabets from the alternatives given below and mark it on your answer - sheet as directed.
18, 24, 21, 27, ?, 30, 27,
33
30
24
21
The correct Answer is:C
To solve the series: 18, 24, 21, 27, ?, 30, 27, we need to identify the pattern in the sequence.
Step 1: Identify the pattern
Let's analyze the series step by step:
1. Start with the first number: 18
2. The second number is 24. This is obtained by adding 6 to 18:
18+6=24
3. The third number is 21. This is obtained by subtracting 3 from 24:
24−3=21
4. The fourth number is 27. This is obtained by adding 6 to 21:
21+6=27
5. Now, we need to find the missing number (let's call it x). According to the pattern, the next operation should be subtracting 3 from 27:
27−3=24
So, x = 24.
6. The sixth number is 30, which is obtained by adding 6 to 24:
24+6=30
7. Finally, the last number is 27, which is obtained by subtracting 3 from 30:
30−3=27
Conclusion
The missing number in the series is 24.
Final Answer
24
Let's analyze the series step by step:
2. The second number is 24. This is obtained by adding 6 to 18:
18+6=24
24−3=21
21+6=27
27−3=24
So, x = 24.
24+6=30
30−3=27
The missing number in the series is 24.
24
Topper's Solved these Questions
- MAT STAGE 2 (2019-20)BOOK - OSWAL PUBLICATIONCHAPTER - MAT STAGE 2 (2019-20)EXERCISE - M.C.Q
97 Videos
- NEW TYPOLOGIES INTRODUCED BY CBSE FOR BOARD 2021-22 EXAM BOOK - OSWAL PUBLICATIONCHAPTER - NEW TYPOLOGIES INTRODUCED BY CBSE FOR BOARD 2021-22 EXAM EXERCISE - UNIT-VII STATISTICS AND PROBABILITY (STATISTICS) (SELF ASSESSMENT)
2 Videos
Similar Questions
In each of the following questions, a series is given, with one term missing. Choose the correct alternative from the given ones that will complete the series.
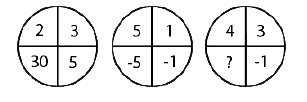
View SolutionIn each of the following questions, a series is given, with one term missing. Choose the correct alternative from the given ones that will complete the series

View Solution
Knowledge Check
In each of the following questions, a series of number / alphabet is given which follow certain rules. One of the number / alphabet is missing. Choose the missing number / alphabets from the alternatives given below and mark it on your answer - sheet as directed.
ELFA, GLHA, ILJA, ? , MLNAAOLPABKLMACLLMADKLLAIn the following question, a series is given with one or more number(s)/alphabet
missing. Choose the correct alternative from the given options.
Cube > Square > ?ALineBTriangleCRectangleDCircleIn the following questions, a series is given with one or more number(s) / alphabet missing. Choose the correct alternative from the given options.
X_ZY_X_YZY_XAXZYZBZYXYCYZXZDYYZZ
In each of the following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.

View SolutionIn the following questions, a series is given with one or more number(s) / alphabet missing. Choose the correct alternative from the given options.
BE, DH, ??, HN, JQ
View SolutionIn the following question, a series is given in which one or more alphabet is missing. Choose the correct alternative from the given options.
ADC, EHG, ILK, ?
View SolutionIn the following question, a series is given with one or more number(s)/alphabet missing. Choose the correct alternative from the given options.
7, 51, 8, 65, 9, ?
View SolutionIn the following questions, a series is given with one or more number(s) / alphabet missing. Choose the correct alternative from the given options.
E-D-C-B , J-H-F-D ,O-L-I-?
View Solution
