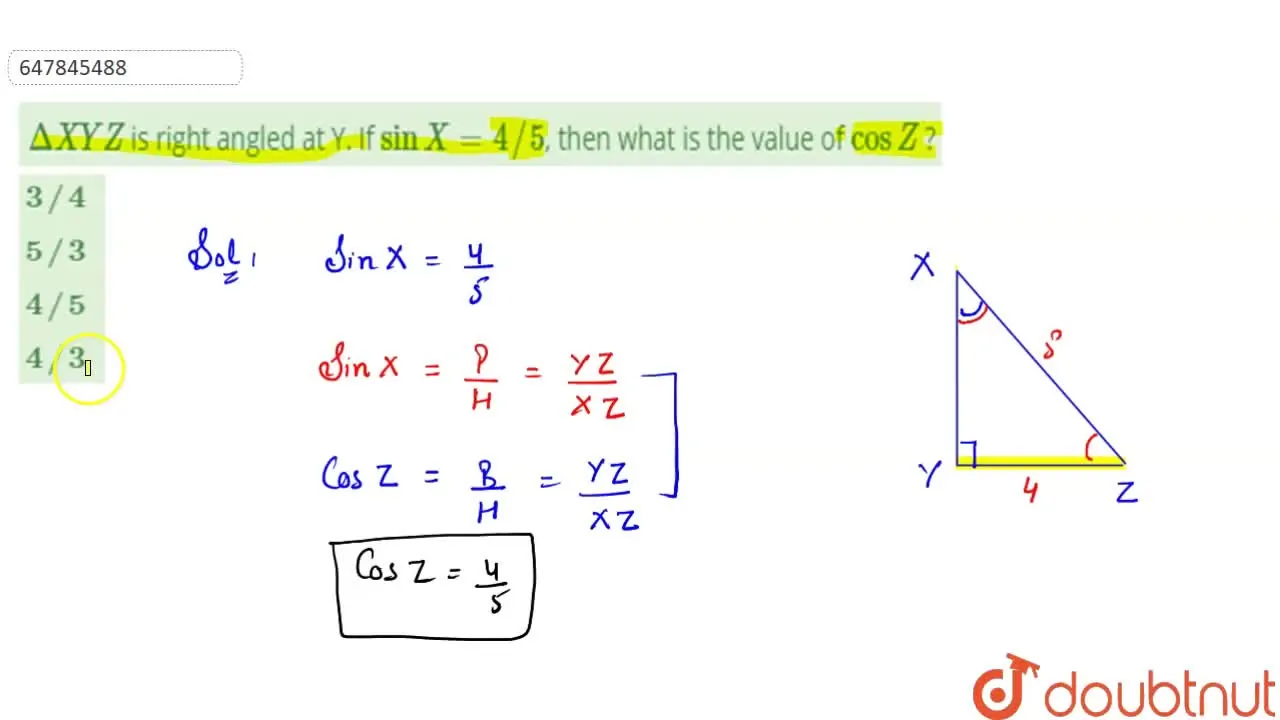
ΔXYZ is right angled at Y. If sinX=4/5, then what is the value of cosZ ?
3/4
5/3
4/5
4/3
The correct Answer is:C
Step by step video, text & image solution for DeltaXYZ is right angled at Y. If sinX=4//5, then what is the value of cosZ ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
ΔXYZ is right angled at Y. If cosX = 3/5, then what is the value of cosecZ ?
View SolutionΔXYZ is right angled at Y. If sinX = 1213, then what is the value of cosecY ?
View SolutionΔUVW is the right angled at V. If sinU=4/5, then what is the value of cosec W?
View SolutionΔXYZ is a right angled at Y. If cotX = 5/12, then what is the value of secZ ?
View SolutionΔXYZ is right angled at Y. If cosec X=1715 ,then what is the value of cotZ?
View SolutionΔXYZ is right angled at Y .If sin X =1213 ,then what is the value of cosec Z?
View Solution△XYZis right angled at Y. If tan X = 24/7, then what is the value of cot Z?
View SolutionΔXYZ is right angled at Y.If tan X =158,then what is the value of sinZ?
View SolutionΔXYZ is right angled at Y.If tan X =158,then what is the value of sinZ?
View SolutionΔDEF is right angled at E. if tanD=12/5, then what is the value of secF?
View Solution