Statement 1 : The plots of probability density and radial probability function versus distance r from the nucleus for any particular orbital are not identical,
Statement 2 : Probability density is ψ2 whereas radial probability function represents probability of finding the electron in a shell of thickness dr.Solution in Malayalam
The correct Answer is:a
The plots are not identical. The probability (ψ2) is along the radial distance whereas radial probability function (4πr2ψ2) is the probability in a shell of thickness dr.
Topper's Solved these Questions
- STRUCTURE OF ATOMSBOOK - BRILLIANT PUBLICATIONCHAPTER - STRUCTURE OF ATOMSEXERCISE - LEVEL - III (Linked Comprehension Type)
8 Videos
- STRUCTURE OF ATOMSBOOK - BRILLIANT PUBLICATIONCHAPTER - STRUCTURE OF ATOMSEXERCISE - LEVEL - III (Matching Column Type)
5 Videos
- STATES OF MATTER BOOK - BRILLIANT PUBLICATIONCHAPTER - STATES OF MATTER EXERCISE - LEVEL III (Linked Comprehension Type )
9 Videos
- THERMODYNAMICS AND CHEMICAL ENERGETICS BOOK - BRILLIANT PUBLICATIONCHAPTER - THERMODYNAMICS AND CHEMICAL ENERGETICS EXERCISE - (LEVEL-II (HOMEWORK)
39 Videos
Similar Questions
The hydrogen-like species Ļi2+ is in a spherically symmetric state S1 with one radial node. Upon absorbing light the ion undergoes transition to a state S2 The state S2 has one radial node and its energy is equal to the ground state energy of the hydrogen atom.
The state S1 is: 1s, 2s, 2p, 3s
View SolutionMatch the orbitals of List-I with the nodal properties of List-II :
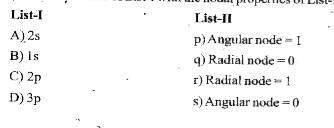
View Solutionwhich of the following statements is correct?
View SolutionWhich of the following is an intensive property
View SolutionOPERATOR FORM SCHRODINGER WAVE EQUATION,PLOT OF RADIAL WAVE FUNCTION 'R',PLOT OF RADIAL PROBABILITY DENSITY 'R^2
View SolutionThe radial probability is the probability of finding electron in a small spherical shell around the nucless at a particular distance ® Hence radial probility is
View SolutionThe variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
View SolutionAssertion. The plots of probability density and radial probability function versus distance r from the nucleus for any particular orbital are not identical Reason. Probability density is Psi^(2) whereas radial probability function represents probability of finding the electron in a shell of thickness dr .
View SolutionWhich of the following plots of radial - probability function 4π2ψ2 is /are correct


View SolutionSelect the correct plot of radial probability function (4πr2R2) for 2s - orbital.
View Solution[" Which among the following "],[" statements is/are correct? "],[qquad [" For all orbitals,the radial "],[" wave function "(Psi)],[" approaches to zero as "r],[" approaches infinity "],[" The radial probability "],[" density "(psi^(2))_(" for "'1s'" orbital is ")],[" maximum at nucleus "],[" The radial distribution "],[" function "(4 pi r^(2)psi^(2))_(" for "'1s'" is ")],[" minimum at nucleus "],[" In plot of radial wave "],[" function "(psi)_(" changes its ")],[" sign at nodes "]]
View SolutionWhich of the following statement concerning concerning probability density (Psi^(2)) and radial distribution function (4 pir^(2) Psi) for a s - orbit of H - like species is correct ?
View SolutionIf P(r) is the radial probability density for a hydrogen atom then the probability that the separation of the electron and proton is between r and r+ dr is
View SolutionThe variation of radial probability density R^2 (r) as a function of distance r of the electron from the nucleus for 3p orbital: (A)(a) (b) (b) (c) (d)
View SolutionRadial probability density function || Illustration OF Radial probability density function
View SolutionThe radial probability is the probability of finding electron in a small spherical shell around the nucleus at a particular distance r. Hence radial probability is
View Solution
