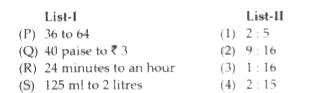In the following question two Quantities i.e., Quantity I and Quantity II are given. You have to determine the relation between Quantity I and Quantity II.
Given, a, b, c and d are positive integers.
I : a−ba−a=ab×c
II : a3×b3a×b2=b3×d4db
Quantity I: Value of ‘c’
Quantity II: Value of ‘d’
Quantity I > Quantity II
Quantity I < Quantity II
Quantity I ≥ Quantity II
Quantity I = Quantity II or no relation can be established
The correct Answer is:D
To solve the given problem, we will analyze both quantities step by step.
Step 1: Solve for Quantity I (Value of 'c')
The equation given is:
a−ba−a=ab⋅c
Using the property of exponents, we can simplify the left side:
a−ba−a=a−b−(−a)=a−b+a=aa−b
Now, we equate this to the right side:
aa−b=ab⋅c
To isolate c, we can divide both sides by ab:
c=aa−bab=a(a−b)−b=aa−2b
Thus, we have:
c=aa−2b
Step 2: Solve for Quantity II (Value of 'd')
The equation given is:
a3⋅b3a⋅b2=b3⋅d4b⋅d
Simplifying the left side:
a3⋅b3a⋅b2=a3a⋅b3b2=a3−1⋅b3−2=a2⋅b
Now simplifying the right side:
b3⋅d4b⋅d=b3b⋅d4d=b3−1⋅d4−1=b2⋅d3
Now we have:
a2⋅b=b2⋅d3
To isolate d, we can rearrange:
d3=a2⋅bb2=a2b
Taking the cube root of both sides gives:
d=√(3)a2b
Step 3: Compare Quantity I and Quantity II
Now we have:
- Quantity I: c=aa−2b
- Quantity II: d=√(3)a2b
Step 4: Determine the relationship between Quantity I and Quantity II
Since a, b, c, and d are all positive integers, we cannot definitively state a relationship between c and d without knowing specific values of a and b. Therefore, we conclude that there is no definitive relationship between Quantity I and Quantity II.
Final Answer:
There is no relation among them.
---
a−ba−a=ab⋅c
a−ba−a=a−b−(−a)=a−b+a=aa−b
aa−b=ab⋅c
c=aa−bab=a(a−b)−b=aa−2b
c=aa−2b
a3⋅b3a⋅b2=b3⋅d4b⋅d
a3⋅b3a⋅b2=a3a⋅b3b2=a3−1⋅b3−2=a2⋅b
b3⋅d4b⋅d=b3b⋅d4d=b3−1⋅d4−1=b2⋅d3
a2⋅b=b2⋅d3
d3=a2⋅bb2=a2b
d=√(3)a2b
- Quantity I: c=aa−2b
- Quantity II: d=√(3)a2b
There is no relation among them.
Similar Questions
Knowledge Check
In the following question two Quantities i.e., Quantity I and Quantity II are given. You have to determine the relation between Quantity I and Quantity II.
‘a’, ‘b’ and ‘c’ are positive integers.
Quantity I: Value of a in (a+b)2−(a−b)28ab(a+b)2=1
Quantity II: Value of c in (c+b)3−(c−b)3(b2+3c2)2=18bAQuantity I > Quantity IIBQuantity I < Quantity IICQuantity I ≥ Quantity IIDQuantity I ≤ Quantity IIMatch the quantities given in List-I with the units given in List-II
 APQRS4321BPQRS3421CPQRS2314DPQRS1234
APQRS4321BPQRS3421CPQRS2314DPQRS1234Some physical quantities are given in the Column I, the related units are given in the Column II. Match the correct pairs in the columns.
 A
A B
B C
C D
D
Four quantities a,b,c d are siad to be proportion if ______
View SolutionMatch the quantity of Column I with the quantity of Column II

View SolutionGiven below are two quantities named I and II. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose among the possible answers.
Quantity I: In a mixture of 80 litre, Milk and water are in the ratio of 7 : 1. If 30% of the mixture is taken out, Find the quantity of the water left in the mixture.
Quantity II: 7 litre
View SolutionGiven below are two quantities named I and II. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose among the possible answers. Quantity I: Age of A is 5 times of his son, after 15 years the ratio of age of A and son is 13 : 5, find the age of A (in years)?
Quantity II: 45
View SolutionGiven below are two quantities named I and II. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose among the possible answers. Quantity I: The average age of a group of students is 24 years. When the age of their teacher is also included, the average age increases by 1 year. If the age of the teacher is 36 years, find the number of students in the group.
Quantity II: 11
View Solution