An aeroplane is flying with a uniform speed of 300 km/h along a circular path. The change in velocity after half the circular track is covered, is given by
300√2 km/h
600 km/h
600√2 km/h
300 km/h
The correct Answer is:B
To find the change in velocity of an aeroplane flying along a circular path after covering half of the circular track, we can follow these steps:
1. Understand the Initial and Final Velocities:
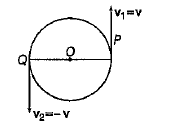
- The aeroplane starts at point A and moves along a circular path. At point A, the velocity (V) is directed tangentially to the circle in a specific direction.
2. Determine the Direction of Velocity at Halfway Point:
- After covering half of the circular path, the aeroplane reaches point B. At this point, the direction of velocity will be directly opposite to that at point A. Therefore, the final velocity (V') at point B is equal in magnitude but opposite in direction to the initial velocity.
3. Express the Initial and Final Velocities:
- Initial velocity (V) at point A = 300 km/h (in a certain direction).
- Final velocity (V') at point B = -300 km/h (in the opposite direction).
4. Calculate the Change in Velocity:
- The change in velocity (ΔV) is given by the formula:
ΔV=V′−V
- Substituting the values:
ΔV=(−300 km/h)−(300 km/h)=−600 km/h
5. Magnitude of Change in Velocity:
- The magnitude of the change in velocity is:
|ΔV|=600 km/h
Final Answer:
The change in velocity after half the circular track is covered is 600 km/h.
---
- The aeroplane starts at point A and moves along a circular path. At point A, the velocity (V) is directed tangentially to the circle in a specific direction.
- After covering half of the circular path, the aeroplane reaches point B. At this point, the direction of velocity will be directly opposite to that at point A. Therefore, the final velocity (V') at point B is equal in magnitude but opposite in direction to the initial velocity.
- Initial velocity (V) at point A = 300 km/h (in a certain direction).
- Final velocity (V') at point B = -300 km/h (in the opposite direction).
- The change in velocity (ΔV) is given by the formula:
ΔV=V′−V
- Substituting the values:
ΔV=(−300 km/h)−(300 km/h)=−600 km/h
- The magnitude of the change in velocity is:
|ΔV|=600 km/h
The change in velocity after half the circular track is covered is 600 km/h.
Similar Questions
Knowledge Check
An aeroplane is flying with a uniform speed of 100 km/h along the circumference of a circle. The change in velocity in half the revolution will be in km/h)
A100B150C200D300An aeroplane is flying with a uniform speed of 100 m/s along a circular path of radius 100 m . the angular speed of the aeroplane will be
A1rad/secB2rad/secC3rad/secD4rad/secIf in aeroplane is moving on a circular path with a uniform speed 300 km /h, then the change in velocity after quarter of the circle will be
A150km/hBzeroC600km/hD300√2km/h
When particle revolves with uniform speed on a circular path
View SolutionAn aeroplane moving in a circular path with a speed 250km/h. The change in velocity in half of the revolution is.
View SolutionA particle moves with uniform speed in a circular path the angle between instantaneous velocity and acceleration is
View SolutionA particle is moving with a constant speed in a circular orbit. Find the change in its velocity when it completes half the revolution.
View SolutionIf a body is moving withuniform speed of 10m/s on a circular path of diameter 2 m , then the difference between the distance covered by it and displacement un half revolution will be
View Solution
