A 200g block while sinking in water, displaces 25g of water. If we leave the block in water independently then, then block will
sink
float with whole volume
partially float
None of the above
The correct Answer is:C
To solve the problem, we need to analyze the situation of the 200g block displacing 25g of water. We will use Archimedes' principle to determine whether the block sinks, floats, or partially floats when placed in water.
1. Understanding the Given Data:
- Mass of the block (m_block) = 200g
- Mass of the water displaced (m_water_displaced) = 25g
2. Applying Archimedes' Principle:
- According to Archimedes' principle, the buoyant force (B) acting on the block is equal to the weight of the water displaced.
- The weight of the displaced water can be calculated as:
B=mwater_displaced⋅g
where g is the acceleration due to gravity. However, since we are comparing masses, we can ignore g for this analysis.
3. Calculating the Buoyant Force:
- The buoyant force is equal to the mass of the water displaced:
B=25g
4. Comparing the Weight of the Block and the Buoyant Force:
- The weight of the block is:
Wblock=mblock=200g
- Now we compare the weight of the block with the buoyant force:
Wblock(200g)>B(25g)
- Since the weight of the block is greater than the buoyant force, the block will not float.
5. Conclusion:
- Since the block is heavier than the buoyant force acting on it, it will sink. However, since it displaces some water, it will not sink completely without any resistance. Therefore, the block will partially float.
Final Answer:
The block will partially float.
- Mass of the block (m_block) = 200g
- Mass of the water displaced (m_water_displaced) = 25g
- According to Archimedes' principle, the buoyant force (B) acting on the block is equal to the weight of the water displaced.
- The weight of the displaced water can be calculated as:
B=mwater_displaced⋅g
where g is the acceleration due to gravity. However, since we are comparing masses, we can ignore g for this analysis.
- The buoyant force is equal to the mass of the water displaced:
B=25g
- The weight of the block is:
Wblock=mblock=200g
- Now we compare the weight of the block with the buoyant force:
Wblock(200g)>B(25g)
- Since the weight of the block is greater than the buoyant force, the block will not float.
- Since the block is heavier than the buoyant force acting on it, it will sink. However, since it displaces some water, it will not sink completely without any resistance. Therefore, the block will partially float.
The block will partially float.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A 200 g block while sinking in water, displaces 25 g of water. If we leave the block in water independently then, the block will
AsinkBfloat with whole volumeCpartially floatDNone of the aboveA 200 g block while sinking in water, displaces 25 g of water. If we leave the block in water independently then, the block will
AsinkBfloat with whole volumeCpartially floatDNone of the aboveWhich body will sink in water? (density of water = 1g cm−3 )
ABody having density of 500kg m−3BBody having density of 988g m−3CBody having density of 125kg m−3DBody having density of 0.85g cm−3
A block flats in water at 40C so that 0.984 of its height is under water. At what temperature of water will the block just sink in water? Negleact expansion of block.
(γRfor water=2.1×10−4/0C)
View SolutionA block hangs from a spring balance. The balance reads 40 N in air, 35 N when block is immersed in water and 25 N when block is immersed in another liquid. Find the density of block and other liquid.
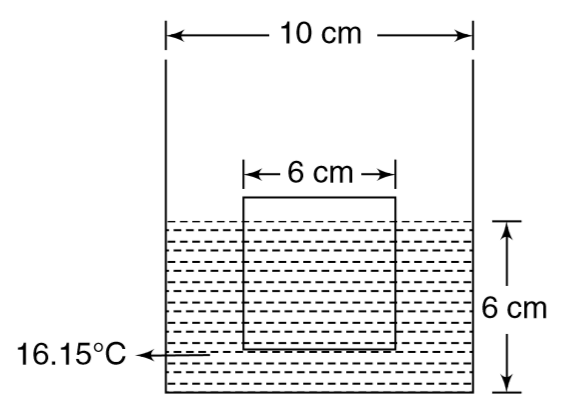
View SolutionA container has a square cross-section of 10cm×10cm. A cubical ice block of side length 6 cm is floating in water in the container. Water level in the container is 6 cm high. The ice block is at a temperature of 0∘C and the water is at 16.15∘C. Assume that heat exchange take place between the ice block and water only. What length of ice block will remain submerged in water when the system reaches thermal equilibrium? Assume that the ice block maintains its cubical shape as it melts. Take - density of ice =0.9g/cc, density of water = 1.0g/cc
Specific heat capacity of water =1calg−1.∘C−1, Specific latent heat of fusion of ice =80calg−1
View SolutionA block of ice is floating in a glass containing water .When the ice melts completely ,the level of the water in the glass will :
View SolutionA boy is carrying a bucket of water in one hand and a wooden block in other hand. If he drops the wooden block in bucket of water then, he will feel thrust
View Solution

