Question

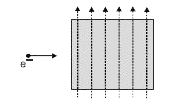
Consider an electron travelling with a speed $V_0$ and entering into a uniform electric field $\overrightarrow{E}$ which is perpendicular to ${\overrightarrow{V}}_0$ as shown in the Figure.

Ignoring gravity, obtain the electron 's acceleration velocity and position as functions of time.

Explanation

The speed of the electrons `v_(0)`
Electric field strength `=vecE`
Acceleration of the electrons a =?
Velocity of the electrons v=?
Position of the electrons r =?
According to Newton.s II law F=ma
The force on the electrons in an uniform electric field.
F=Ee
The `e^(-)` s acceleration due to electric field
`a=(F)/(m)=(Ee)/(m)`
The acceleration of the electrons `[a=(Ee)/(m)]` is in the down direction. The horizontal velocity remains `v_(0)` as there is no acceleration in this direction.
`veca=-(eE)/(m).hatj`
The downward component of the velocity of the electrons as it emerges from the field region is
`v=v_(x)hati+v_(y)hatj`
The horizontal component of the velocity remains `v_(x)=v_(0)`. The vertical component (downward) velocity as it emerges from the field region is
`v_(y)=vecat=-(eE)/(m)t.hatj`
The velocity of the `e^(-)=v_(0)hati-(eE)/(m).t.hatj`
The electrons starts with a velocity `v_(0)`.
From equation of motion, `s=ut+(1)/(2)at^(2)`
The position of the electrons s=r = ?
Initial velocity of the electrons u=`v_(0)`
Acceleration of the electrons `vec(a)=(-(eE)/(m))t.hatj`
`:.vecr=v_(0)thati+(1)/(2).(-(Ee)/(m)t).hatj`
`=v_(0)thati-(1)/(2).(Ee)/(m).t^(2)hatj`
`vec(r)=v_(0)thati-(1)/(2).(Ee)/(m).t^(2)hatj`.