Find the matrices of transformation T1T2andT2T1 when T1 is rotated through an angle 60∘andT2 is the reflection in the Y-asix Also, verify that T1T2≠T2T1. Solution in Kannada
T1=[cos60∘,−sin60∘sin60∘,cos60∘]=⎡⎢⎣12−√32√3212⎤⎥⎦=12[1√3−√31]
and T2=[−1001]
∴ T1T2=12[1−√3√31]×[−1001]=12[−1+00−√3−√3+00+1]
=12[1−√3−√31]=⎡⎢⎣−12−√32−√3212⎤⎥⎦
T1T2=[−1001]×12[1−√3√31]=12[−1+0√3+00+√30+1]
=12[−1√3√31]=⎡⎢⎣−12√32√3212⎤⎥⎦
it is clear from Eqs. (i) and (ii) , then
T1T2≠T2T1
Similar Questions
यदि (x+a)n के विस्तार में, T0,T1,T2,…. पद प्राप्त होते है, तो (T0−T2+T4−…)2+(T1−T3+T5−….)2 बराबर होगा
View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
View SolutionThe tangents at the points (at21,2at1),(at22,2at2) are right angles if
View Solution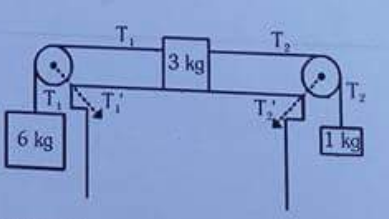
Calculate a, T1,T2,T1'&T2'.
View SolutionIf the normals at P(t_(1))andQ(t_(2)) on the parabola meet on the same parabola, then (A) t_(1)t_(2)=-1 (B) t_(2)=-t_(1)-(2)/(t_(1)) (C) t_(1)t_(2)=1 (D) t_(1)t_(2)=2
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)],[at2,a(t2+t3)] and [at3t1,a(t3+t1)]. The co ordinates of the orthocentre of the triangle are…….
View SolutionA point moving in a straight line with uniform acceleration describes aand b feet in successive intervals of t1 and t2 seconds. Then the acceleration is 2(bt1−at2)t1t2(t1+t2)
Also if the point describes equal distances in successive times t1,t2,t3 then
1t1−1t2+1t3=3t1+t2+t3
View Solution
Calculate a, T1,T2,T1'&T2'.
View Solution
