Let OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel as shown in figure. Also, OA:CB=2:1 and OD:AB=1:3. if the diagonals OC and AD meet at x, find OX:XC.Solution in Kannada
The correct Answer is:
Let O be the origin of reference.
Let the position vectors of A,B,C and D be a,b,c and d,
respectively.
then,

. . . (i)
and
[using eq. (i)]
. . . (ii)
Let OX:XC=
Now, X divides OC in the ratio . therefore,
PV of . . . (iii)
X also divides AD in the ratio
PV of X
from eqs. (iii) and (iv), we get
[using eqs. (i) and (iv)]
(since, b and c are non-collinear)
Hence,
Similar Questions
आकृति में, ABCD एक समलम्ब चतुर्भुज हैं, जिसमें भुजा AB भुजा DC के समान्तर हैं तथा E भुजा AD का मध्य-बिंदु हैं। E भुजा BC पर इस प्रकार है खंड EF, भुजा DC के समान्तर हैं। सिद्ध कीजिए कि EF=12(AB+DC)
View Solutionकिसी समांतर चतुर्भुज ABCD में यदि विकर्णों का कटान-बिंदु O हो और OC = 6 सेमी, OB = 8 सेमी तो OA, OD, AC एवं BD के मान निकालिए।
View SolutionThe following figure shows a trapezium ABCD in which AB is parallel to DC and AD= BC
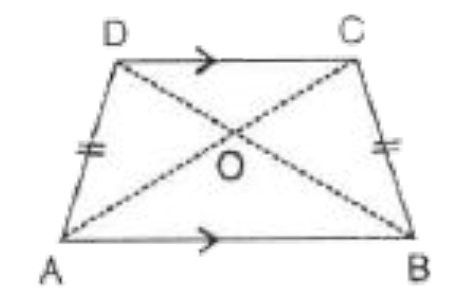
Prove that:
OA = OB and OC= OD
View SolutionAB and BD are two parallel sides of trapezium ABCD. if the diagonals AC and BD meet at O, then prove that (AO)/(OC) = (BO)/(OD) .
View SolutionThe side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides.

Also, find :
the slope of the diagonal AC.
View SolutionThe side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides.

Also, find :
the slope of the diagonal BD.
View SolutionThe diagonals of a square ABCD intersect at O. If the length of each sides of the square is 6cm then find the value of OA2+OB2+OC2+OD2.
View SolutionLet OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel. Also OA:CB=2:1andOD:AB=1:3.

The ratio OXXC is
View Solution