In a regular hexagon ABCDEF, prove that AB+AC+AD+AE+AF=3AD.Solution in Kannada

A

2

B

3

C

4

D

6

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

By triangle law, $A B = A D - B D, A C = A D - C D$

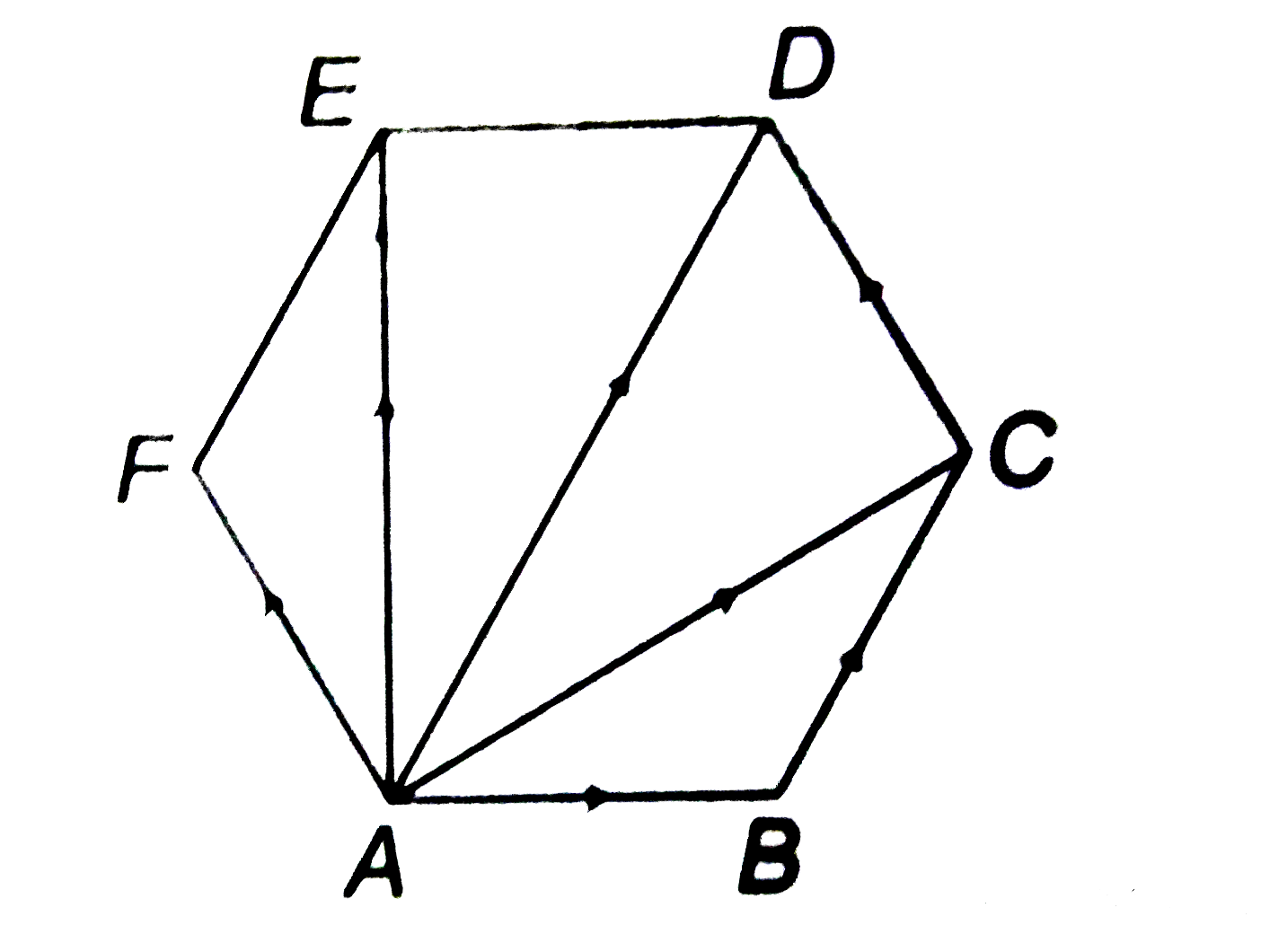
Therefore, $A B + A C + A D + A E + A F$
$= 3 A D + (A E - B D) + (A F - C D) = 3 A D$
hence, $λ = 3 (∵ A E = B D, A F = C D)$

Updated on:21/07/2023

|

Class 12 MATHS VECTOR ALGEBRA

Similar Questions

ABCDEF is a regular hexagone. $A B + A C + A D + A E + A F = λ A D$ then $λ$ = ………….
View Solution
In a regular hexagon $A B C D E F, ¯ ¯¯¯¯ ¯ A B + ¯ ¯¯¯¯ ¯ A C + ¯ ¯¯¯¯ ¯ A D + ¯ ¯¯¯¯ ¯ A E + ¯ ¯¯¯¯ ¯ A F = k ¯ ¯¯¯¯ ¯ A D$ then k is equal to
View Solution
Consider the regular hexagon ABCDEF with centre at O (origin).
Q. Five forces AB,AC,AD,AE,AF act at the vertex A of a regular hexagon ABCDEF. Then, their resultant is (a)3AO (b)2AO (c)4AO (d)6AO
View Solution
In a regular hexagon ABCDEF, prove that $- - \to A B + - - \to A C + - - \to A D + - - \to A E + - - \to A F = 3 - - \to A D$
View Solution
Consider the regular hexagon ABCDEF with centre at O (origin). Five forces vec(AB), vec(AC), vec(AD), vec(AE), vec(AF) act at the vertex A of a regular hexagon ABCDEF. Then their resultant is
View Solution
ABCDEF is a regular hexagon. Find the vector $\to A B + \to A C + \to A D + \to A E + \to A F$ in terms of the vector $\to A D$
View Solution
In a regular hexagon $A B C D E F, - - \to A B + - - \to A C + - - \to A D + - - \to A E + - - \to A F = k - - \to A D$ then k is equal to
View Solution
Consider the regular hexagon ABCDEF with centre at O (origin).
Five forces AB,AC,AD,AE,AF act at the vertex A of a regular hexagon ABCDEF. Then, their resultant is
View Solution

Recommended Questions

Home
Ask Doubt
Profile