The direction (θ) of →E at point P due to uniformly charged finite rod will be
 Solution in Kannada
Solution in Kannada
The correct Answer is:A, B, C, D
(A) Let ˆiandˆj be the unit vectors along OX and OY respectively.
Now, OP=3 and a∩g≤XOP=45∘ implies that
OP=(3cos45∘)ˆi+(3sin45∘)ˆj=3√2(ˆi+ˆj)
(B) Again ∠XOR=135∘andOR=4 implies that
OR=4√2(−ˆi+ˆj)=2√2(−ˆi+ˆj)
(C) the position vector of Q is given by
OP+PQ=OP+OR=1√2(−ˆi+7ˆj)
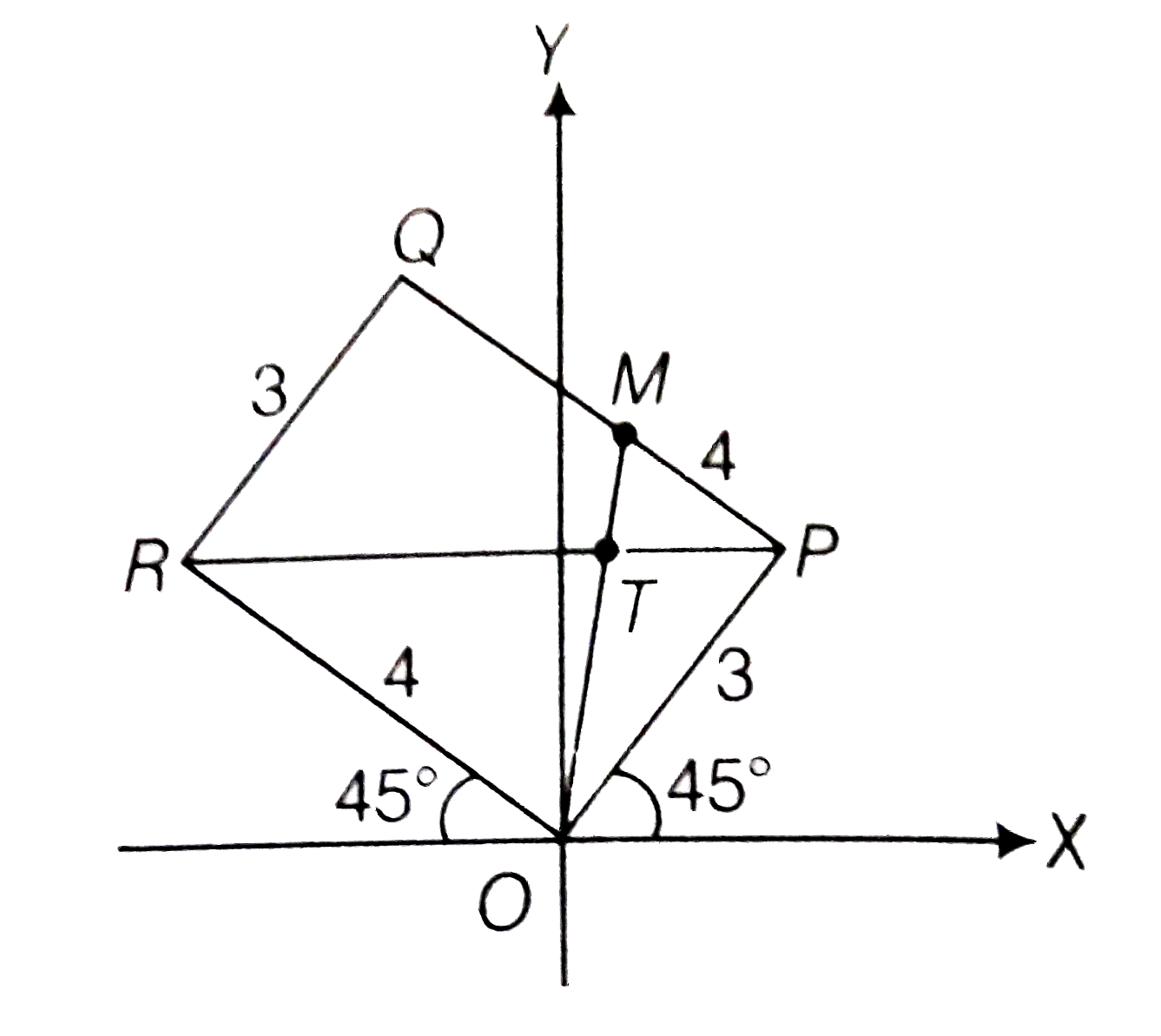
∴OM=(3√2)(ˆi+ˆj)+(1√2)(−ˆi+7ˆj)2
=2ˆi+10ˆj2√2=ˆi+5ˆj√2
(D) Now, PT:RT=1:2
thereofore, OT=1(OR)+2(OP)3
=(4√2)(−ˆi+ˆj)+2[(3√2)(ˆi+ˆj)]3
=√23(ˆi+5ˆj)
Similar Questions
The inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionAt point P, the value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_025_Q01.png" width="80%"gt
View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt
View SolutionMatch column I with column II:
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C18_E01_003_Q01.png" width="80%"gt
View SolutionAt point P, the value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_025_Q01.png" width="80%"gt
View Solution