In a quadrilateral PQRS,→PQ=→a,→QR=→b,→SP=→a−→b,M is the midpoint of →QRandX is a point on SM such that SX=45SM. Prove that P,XandR are collinear.Solution in Kannada
PX=15PR
PX=35PR
PX=25PR
none of these
The correct Answer is:B
If we take point P as the origin, the position vectors of Q and S are a and b-a respectively.
In ΔPQR, we have
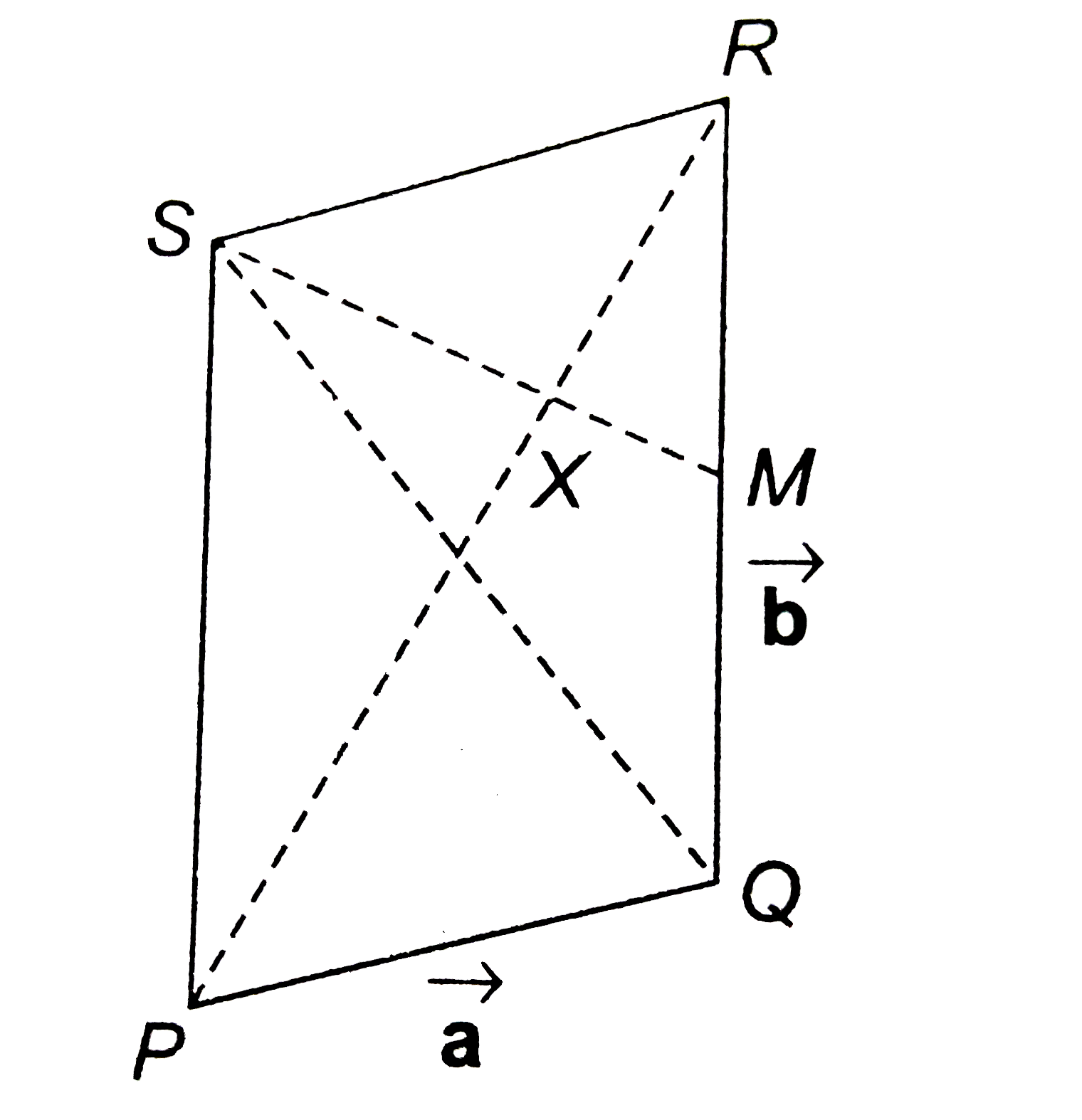
PR=PQ+QR⇒PR=a+b
∴Position vector of R=a+b
⇒PV or M=a+(a+b)2=(a+12b)
Now, SX=45SM
⇒XM=SM−SX=SM−45SM=15SM
∴SX:XM=4:1
⇒PV of X=4(a+12b)+1(b−a)4+1
=3a+2b5⇒PX=35(a+b)
⇒PX=35PR
Similar Questions
Suppose that →p,→qand→r are three non-coplanar vectors in R. Let the components of a vector →s along →p,→qand→r be 4, 3 and 5 respectively. If the components of this vector →s along(−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x,y and z respectively, then the value of 2x+y+z is
View SolutionThe projection of point P(→p) on the plane →r.→n=q is (→s) , then a. →s=(q−→p.→n)→n|→n|2 b. →s=p+(q−→p.→n)→n|→n|2 c. →s=p−(→p.→n)→n|→n|2 d. →s=p−(q−→p.→n)→n|→n|2
View SolutionIf P,Q and R are three collinear points such that →PQ=→a and →QR = →b. Find the vector →PR .
View SolutionIf vec P+ vec Q = vec R and |vec P| = |vec Q| = | vec R| , then angle between vec P and vec Q is
View SolutionIf →P+→Q=→Rand→P−→Q=→S, then R2+S2 is equal to
View SolutionIf vec(P) + vec(Q) = vec(R) and vec(P) - vec(Q) = vec(S) , then R^(2) + S^(2) is equal to
View SolutionThe projection of point P(→p) on the plane →r.→n=q is (→s) , then a. →s=(q−→p.→n)→n|→n|2 b. →s=p+(q−→p.→n)→n|→n|2 c. →s=p−(→p.→n)→n|→n|2 d. →s=p−(q−→p.→n)→n|→n|2
View SolutionProve that [vec(p) - vec(q) vec(q) - vec(r) vec(r) - vec(p)] = 0
View Solution
