Let α,β,γ are distinct real numbers. The points with position vectors αi+βj+γk, βi+γj+αk, γi+αj+βkSolution in Kannada
are collinear
form an equilateral triangle
form a scalene triangle
form a right angled triangle
Let given point be A, B and C with positive vectors αˆi+βˆj+γˆk,βˆi+γˆj+αˆkandγˆi+αˆj+βˆk
As α,βandγ are distinct real numbers, therefore ABC form a triangle.
Clearly, AB=OB−OA=(βˆi+γˆj+αˆk)−(αˆi+βˆj+γˆk)
=(β−α)ˆi+(γ−β)ˆj+(α−γ)ˆk
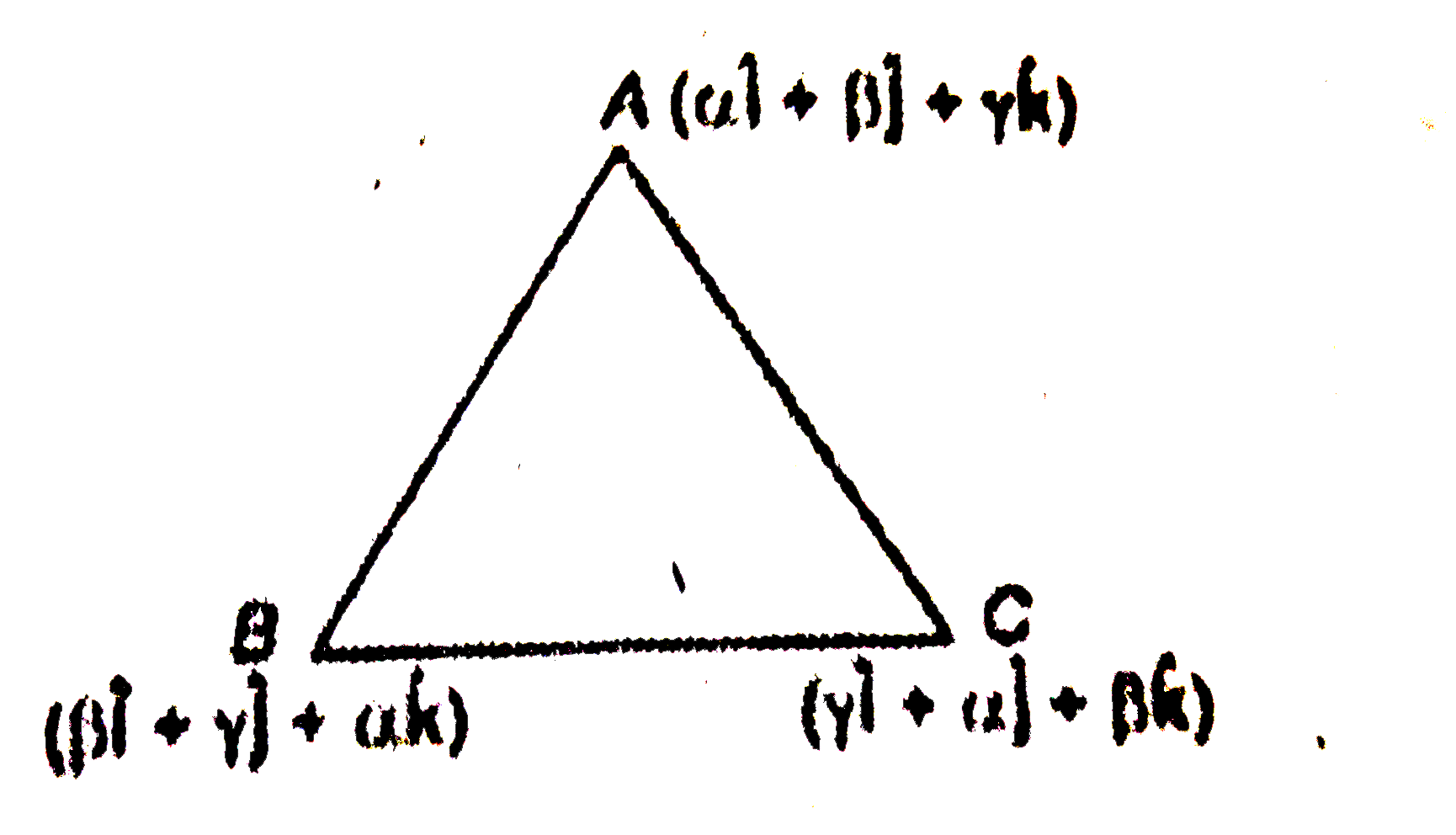
Now, |AB|=√(β−α)2+(γ−β)2+(α−γ)2
Similarly, BC=CA=√(β−α)2+(γ−β)2+(α−γ)2
∴ΔABC is an equilateral triangle.
Similar Questions
The point (α,β,γ) lies on the plane x+y+z = 2. Let, →a=αi+βj+γk and k×(k×→a)=→0 then γ=
View SolutionConsider the vectors ˆi+cos(β−α)ˆj+cos(γ−α)ˆk,cos(α−β)ˆi+ˆj+cos(γ−β)ˆkandcos(α−γ)ˆi+cos(β−γ)ˆk+aˆkwhere α,β, and γ are different angles. If these vectors are coplanar, show that a is independent of α,β and γ
View SolutionLett α,βandγ be distinct real numbers. The points whose position vector's are αˆi+βˆj+γˆk;βˆi+γˆj+αˆkandγˆi+αˆj+βˆk
View SolutionConsider the vectors ˆi+cos(β−α)ˆj+cos(γ−α)ˆk,cos(α−β)ˆi+ˆj+cos(γ−β)ˆk and cos(α−γ)ˆi+cos(β−γ)ˆj+aˆkwhere α,β, and γ are different angles. If these vectors are coplanar, show that a is independent of α,β and γ
View SolutionLet α,βandγ be distinct real numbers. The points whose position vector's are αˆi+βˆj+γˆk;βˆi+γˆj+αˆkandγˆi+αˆj+βˆk a. are collinear. b. forms an equilateral triangle. c. forms a scalene triangle. d. forms a right angled triangle.
View SolutionIf α=2i+3j−k,β=−i+2j−4k,γ=i+j+k then the value of (α×β).(α×γ) is equal to
View SolutionIf α=2i+3j−k,β=−i+2j−4k,γ=i+j+k then the value of (α×β).(α×γ) is equal to
View SolutionIf the vectors alpha hat(i) + alpha hat(j) + gamma hat(k). hat(i) + hat(k) and gamma hat(i) + gamma hat(j) + beta hat(k) lie on a plane. Where alpha, beta and gamma are distinct non-negative numbers, they gamma is:
View Solution
