An investigator interviewed 100 students to determine their preferences for the three drinks, milk (M), coffee (C ) and tea (T). He reported the following: 10 students has all three drinks M, C, T, 20 had M and C, 30 had C and T, 25 had M and T, 12 had M only, 5 had C only and 8 had T only. Using a Venn diagram, find how many did not take any of the three drinks? Solution in Kannada
Given, M, C and T are the sets of drinks, milk, coffee and tea, respectively. Let us denote the number of drinks (students) contained in the bounded region as shown in the diagram by a, b, c, d, e, f and g, respectively.
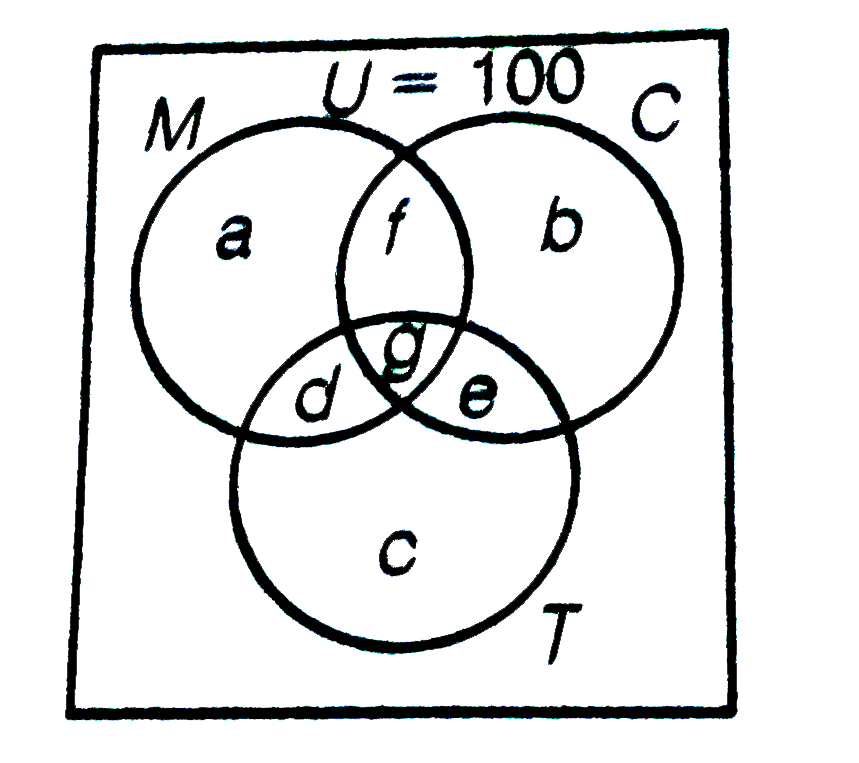
Then, g = 10
g + f = 20 implies f = 10 [∵g=10]
g + e = 30 implies e = 20
d + g = 25 implies d = 15
and a = 12, b = 5, c = 8
Thus, total number of students taking drinks M or C or T
= a + b + c + d + e + f + g
= 12 + 5 + 8 + 15 + 20 + 10 + 10 = 80
Hence, the number of students taking none of them drinks
= 100 - 80 = 20
Similar Questions
An investigator interviewed 100 students to determine their preferences for the three drinks : milk (M) , coffee (C ) and tea (T) . He reported the following : 10 students had all the three drinks M, C, T , 20 had M and C only , 30 had C and T , 25 had M and T , 12 had M only , 5 had C only , 8 had T only . Find how many did not take any of the three drinks
View SolutionQ.N. 45 In a survey of 25 students ,it was found that 15 had taken mathematics , 12 had taken physics and 11 had taken chemistry ,5 had taken mathematics and chemistry, 9 had taken mathematics and physics, 4 had taken physics and chemistry and 3 had taken all the three subjects. write the number of student that had taken (a) at least one of three subjects (b) only mathematics
View SolutionAn investigator interviewed 100 students to determine the performance of three drinks: that 10 students take all three drinks milk, milk, coffee and tea. The investigator reported coffee and tea; 20 students take milk and coffee: 25 students take milk and tea; 20 students take coffee and tea; 12 students take milk only; 5 students take coffee only and 8 students take tea only. then the number of students who did not take any of three drinks is
View Solutionदो संख्याओं का म. स. यदि उनमें से ही एक संख्या उनका ल. स. दूसरी संख्या होगा|
View SolutionIn a group of 50 persons, 14 drink tea but not coffee and 30 drink tea. Let T and C denote the sets of persons drinking tea and coffee respectively.What is the value of n (T - C)?
View SolutionIn a group of 50 persons, 14 drink tea but not coffee and 30 drink tea. Let T and C denote the sets of persons drinking tea and coffee respectively.What is the value of n (T)?
View SolutionIn a group of 50 persons, 14 drink tea but not coffee and 30 drink tea. Let T and C denote the sets of persons drinking tea and coffee respectively.How many drink tea and coffee both?
View SolutionIn a group of 50 persons, 14 drink tea but not coffee and 30 drink tea. Let T and C denote the sets of persons drinking tea and coffee respectively.How many drink coffee but not tea?
View Solution
