Find the number of triangles whose angular points are at the angular points of a given polygon of n sides, but none of whose sides are the sides of the polygon.Solution in Kannada
A polygon of n sides has n angular points. Number of triangles formed from these n angular points=.nC3.
These are comprised of two exclusive cases viz.
(i) atleast one side of the triangle is a side of the polygon.
(ii) no side of the triangle is a side of the polygon.
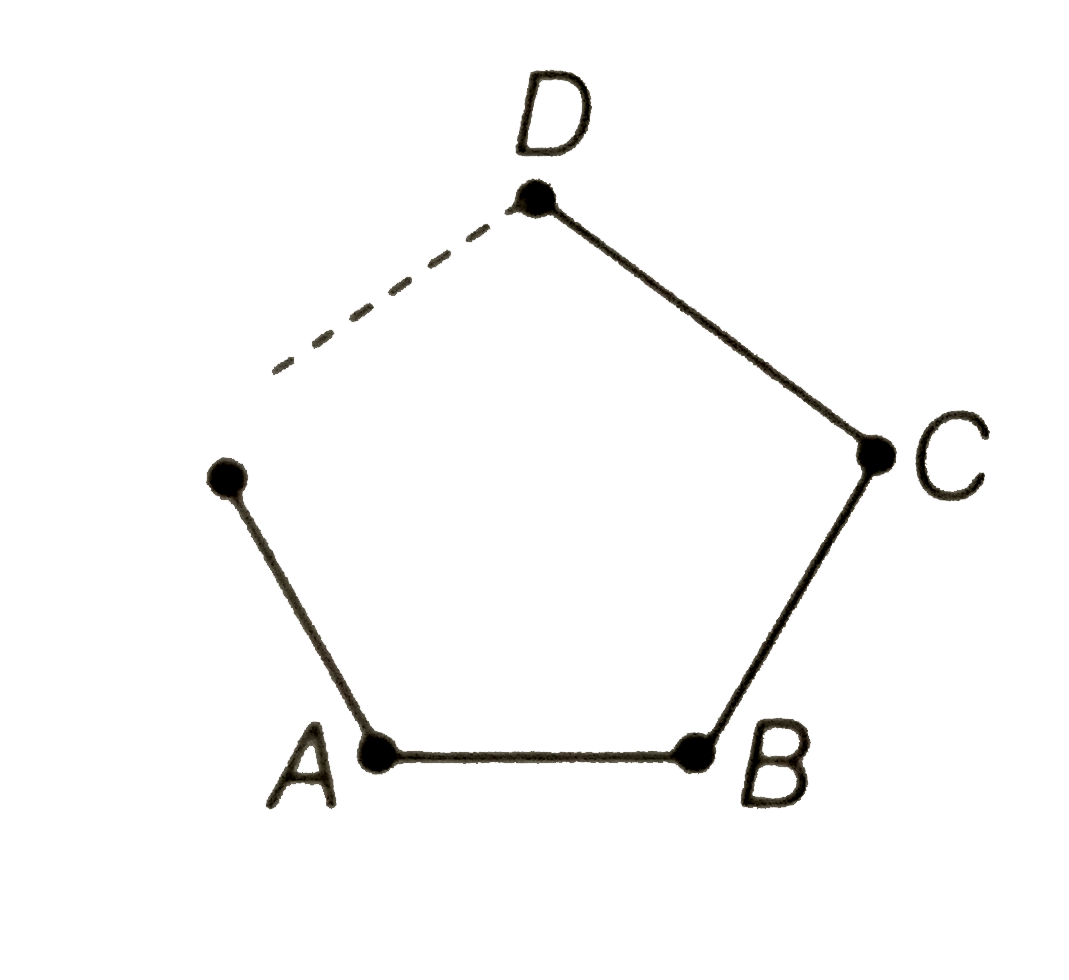
Let AB be one side of the polygon. if each angular point of the remaining (n-2) points are joined with A and B, we get a triangle with one side AB.
∴Number of triangles of which AB is one side=(n-2)
Likewise, number of triangles of which BC is one side=(n-2) and of which atleast one side is the side of the polygon=n(n-2).
Out of these triangle, some are counted twice. for example, the triangle when C is joined with AB is ΔABC, is taken when AB is taken as one side. again triangle formed when A is joined with BC is counted when BC is taken as one side.
So, the number of triangles of which one side is the side of the triangle.
=n(n−2)−n=n(n−3)
=.nC3−n(n−3)=16n(n−4)(n−5)
Similar Questions
A regular polygon of 10 sides is constructed. Triangles are formed joining vertices of the polygon. Find the number of triangles
(i) if two sides of trinangle coincide with the sides of polygon.
(ii) if only one side of triangle coincide with the side of polygon.
View SolutionThree vertices of a convex polygon of n sides are chosen. If the number of triangles that can be drawn is such that no side of the triangle is the side of the polygon. Is 30, then the polygon is
View SolutionIf number of triangles joining angular points of a n-sided polygon be 12n.find n
View SolutionIn a n sided polygon joining by straight line all the angular points. . and obtained, the triangles are in number 5n' Find the value of n.
View SolutionFind the numbers of sides of a polygon whose number of diagonals is
5
View SolutionFind the numbers of sides of a polygon whose number of diagonals is
14
View SolutionFind the numbers of sides of a polygon whose number of diagonals is
27
View SolutionThe equation of the sides of a triangle, the coordinates of whose angular points are: (3,5),(1,2) and (−7,4).
View Solution
