Question

Let a $\in$ R and f : $R\to R$ be given by $f\left(x\right)=x^5-5x+a$, then
(a) $f\left(x\right)=0$ has three real roots if $a>4$
(b) $f\left(x\right)=0$ has only one real root if $a>4$
(c) $f\left(x\right)=0$ has three real roots if $a<-4$
(d) $f\left(x\right)=0$ has three real roots if $-4<a<4$

Options

A. (a) `f(x)` has three real roots if `agt4`
B. (b) `f(x)` has only one real root if `agt4`
C. (c) `f(x)` has three real roots if `alt-4`
D. (d) `f(x)` has three real roots if `-4ltalt4`

Answer

D

Explanation

`f(x)=x^(5)-5x` and `g(x)=-a`
`:.f'(x)=5x^(4)-5`

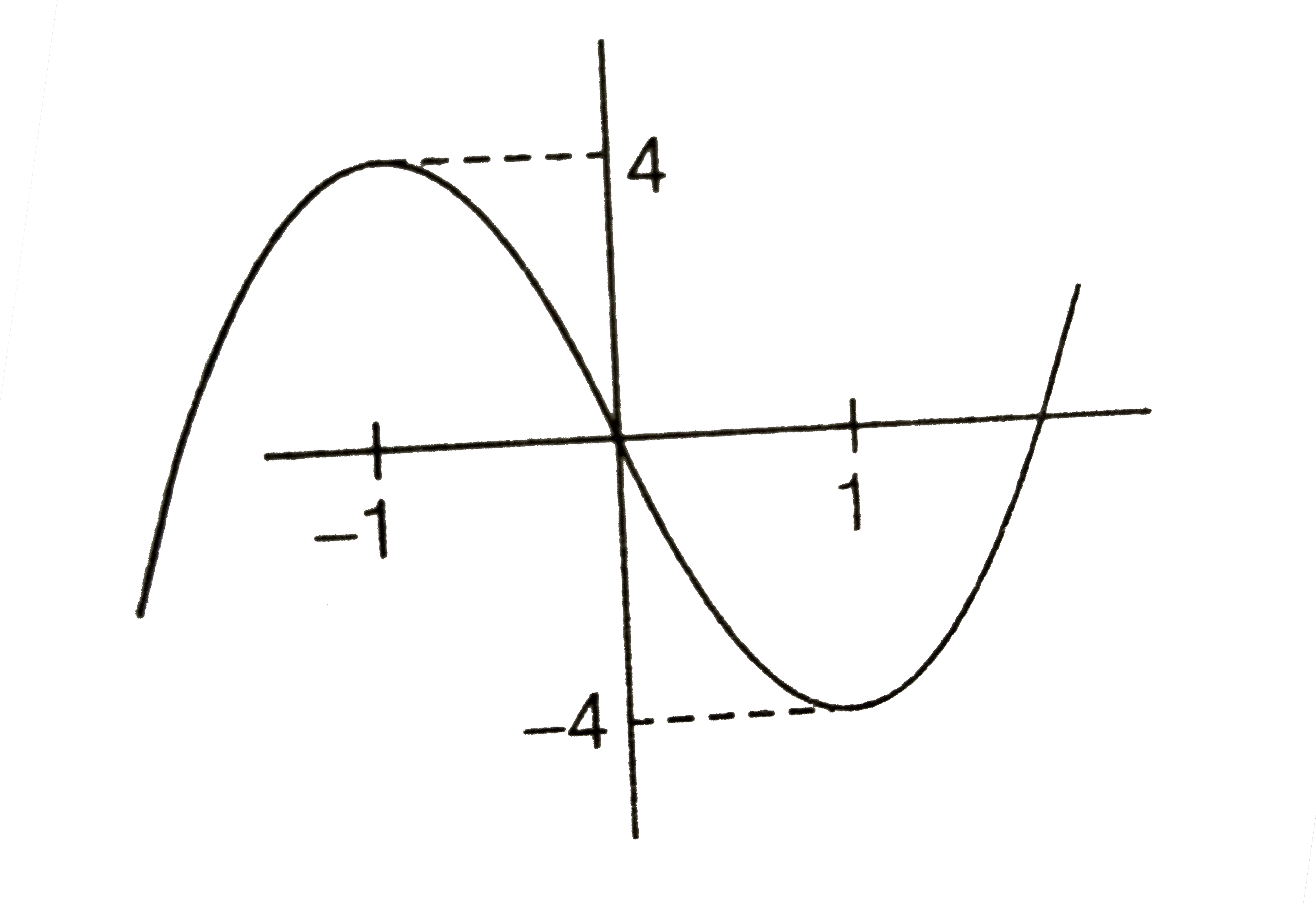
`=5(x^(2)+1)(x-1)(x+1)`
Clearly `f(x)=g()` has one real root, if `a gt4` and three real roots if `|a|lt4`.