If are the roots of the equation and are the roots of the equation
such that find the value of .Solution in Kannada
The correct Answer is:
Since the given equation is
or
and
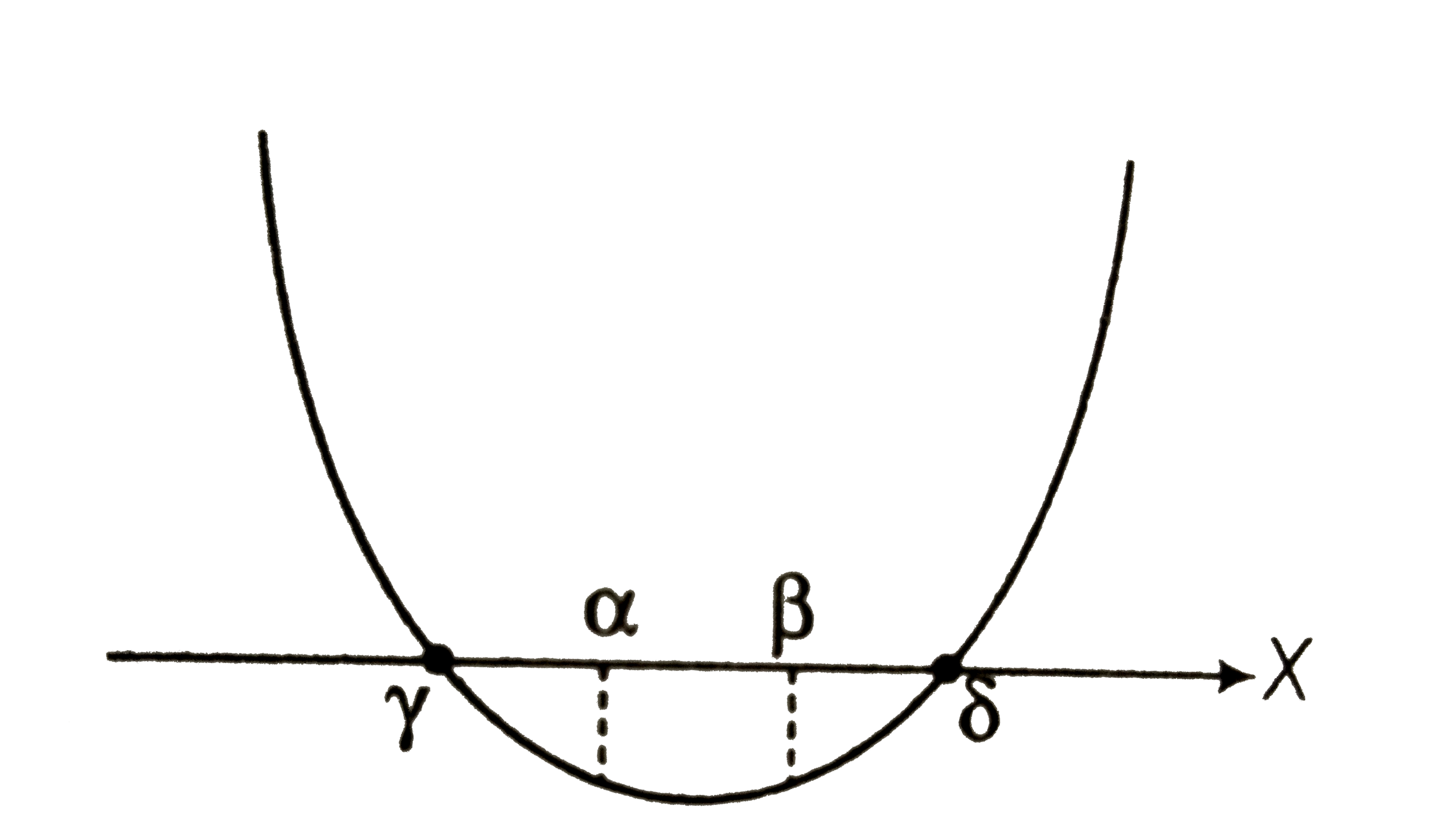
Let thus the following conditiions hold good:
Consider the followign cases:
Case I
Case II
Case II
Combining all cases we get
Similar Questions
यदि α और β समीकरण x2+px−q=0 के तथा γ,δ समीकरण x2+px+r=0 के मूल हैं, तो सिद्ध कीजिए की, (α−γ)(α−δ)=(β−γ)(β−δ)=q+r
06:06View SolutionIf α,β,γandδ are the roots of the equation x4−bx−3=0, then an equation whose roots are α+β+γδ2,α+β+δγ2,α+δ+γβ2,andδ+β+γα2, is:
06:43View SolutionIf α,β are the roots of x2+px+1=0 and γ,δ are the roots of x2+qx+1=0 then (α−γ)(β−γ)(α+δ)(β+δ)=
05:43View SolutionIf αandβ are the roots of the equation x2+px+1=0,gamam,δ are the roots of (x2+qx+1=0 , then , find (α−γ)(β−γ)(α+δ)(β+δ)
06:05View SolutionIf αandβ are the roots of x2+qx+1=0 and γ,δ the roots of x2+qx+1=0, then the value of
(α−γ)(β−γ)(a+δ)β+δ) is :02:42View SolutionIf α,β be the roots of x2+x+2=0 and γ,δ be the roots of x2+3x+4=0 then (α+γ)(α+δ)(β+γ)(β+δ)=
09:13View SolutionIf α,β,γandδ are the roots of the equation x4−bx−3=0, then an equation whose roots are α+β+γδ2,α+β+δγ2,α+δ+γβ2,andδ+β+γα2, is:
04:28View SolutionIf α,β be the roots of x2+x+2=0 and γ,δ be the roots of x2+3x+4=0, then (α+γ)(α+δ)(β+γ)(β+δ) is equal to
View Solution
