In the given figure vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.
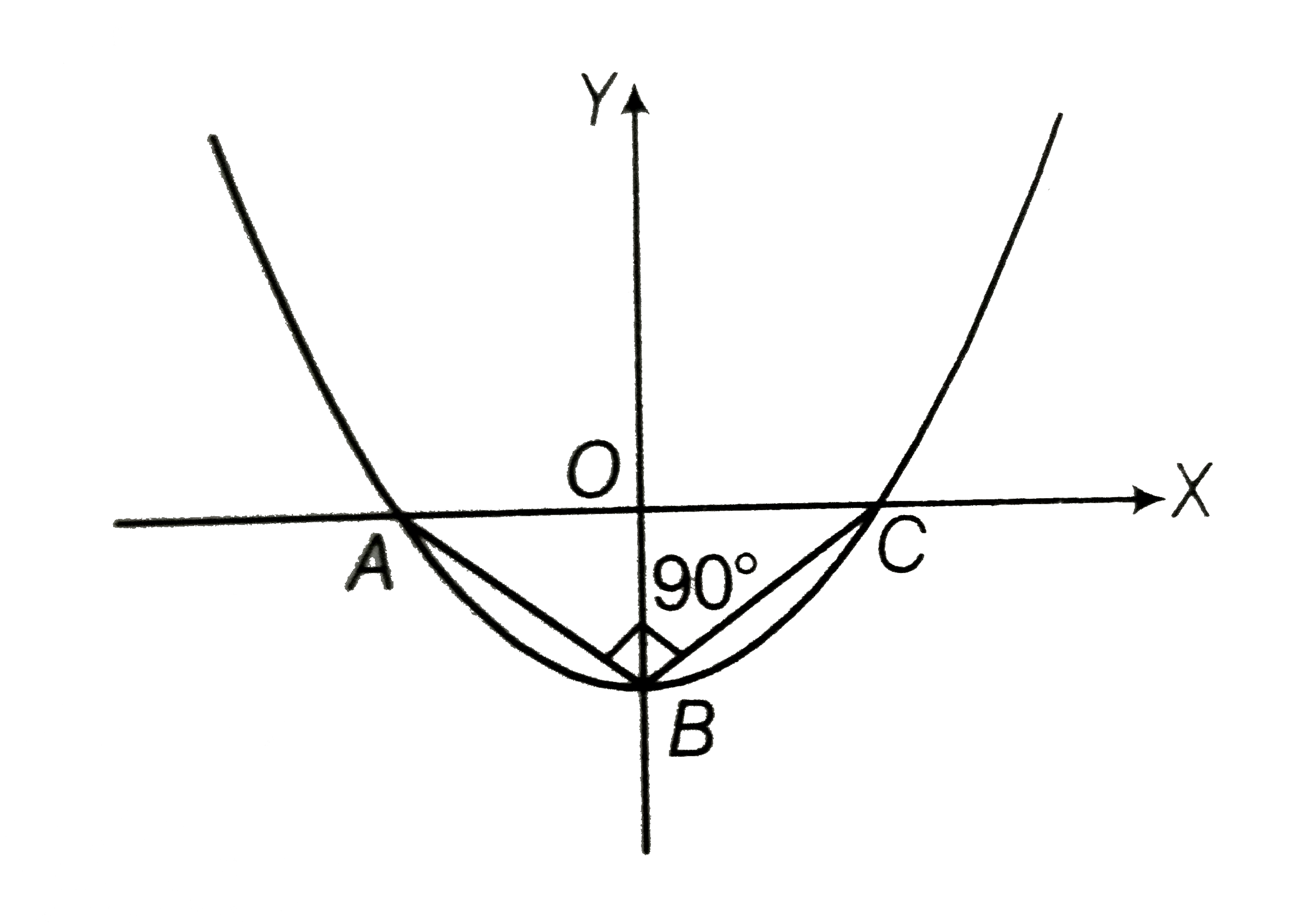
y=f(x) is given by Solution in Kannada
9
10
11
12
The correct Answer is:C
Given that AC=4√2 units
∴AB=BC=AC√2=4 units andd OB=√(BC)2−(OC)2
=√(4)2−(2√2)2[∵OC=AC2]
=2√2 units
∴ Vertices are A=(−2√2,0),
B=−(0,−2√2)
and C=(2√2,0)
f(x)=0
⇒x22√2−2√2=0⇒x=±2√2
Given −2√2<λ2lg2√2
or −4√2<λ<4√2
∴ Initial values of λ are −5,−4,−3,−2,−1,0,1,2,3,4,5
∴ Number of integral values is 11.
Similar Questions
दिये गये चित्र में ΔABC के शीर्ष y=f(x)=ax2+bx+c पर स्थित है ΔABC समकोण समद्विबाहु त्रिभुज है जिसका कर्ण AC=4√2 इकाई है, तब
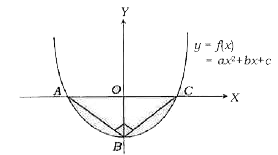
k के पूर्णांक मानों की संख्या जिसके लिए k2,f(x)=0 के मूलों के बीच स्थित है
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.

y=f(x) is given by
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.
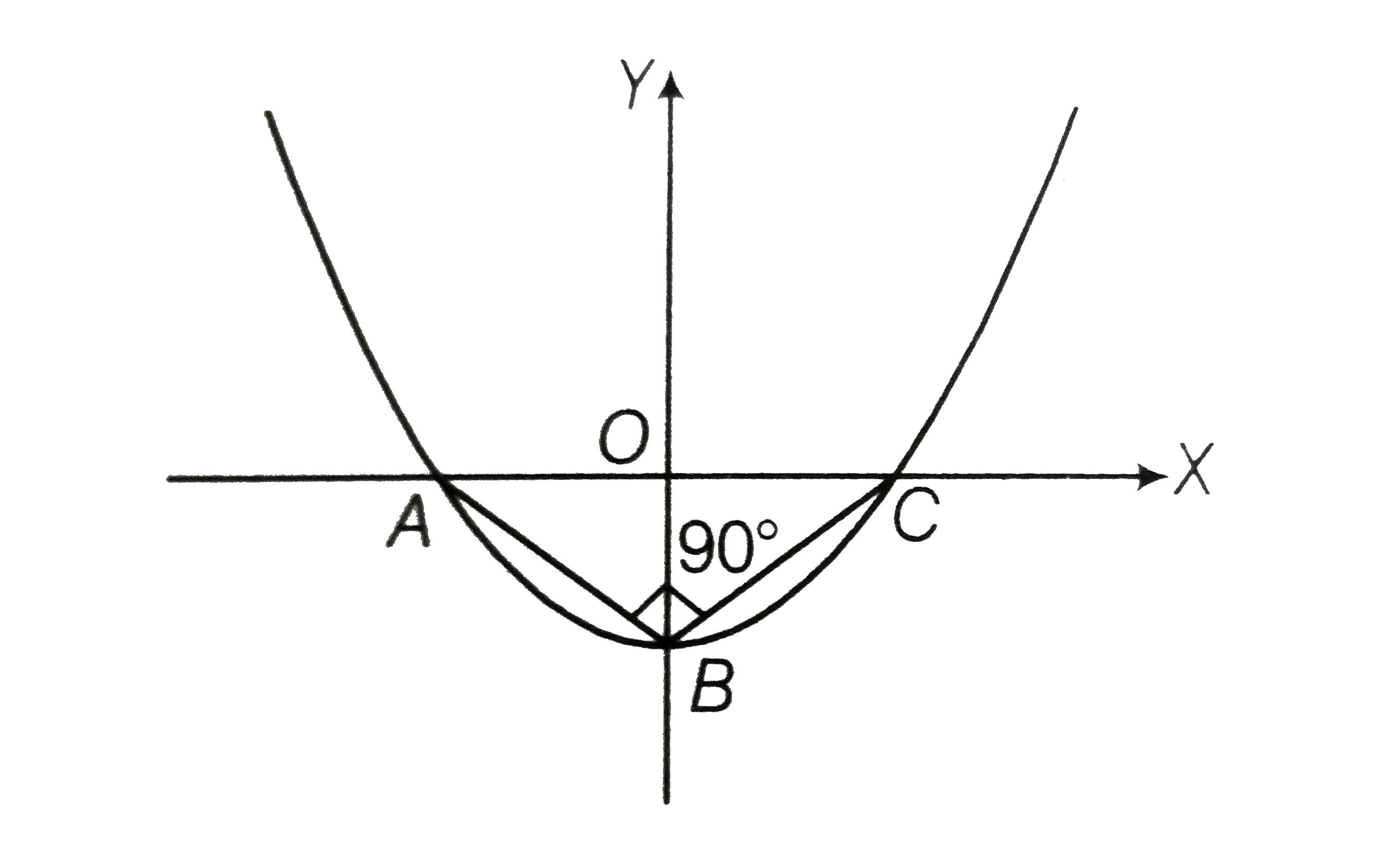
Minimum valueof y=f(x) is
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
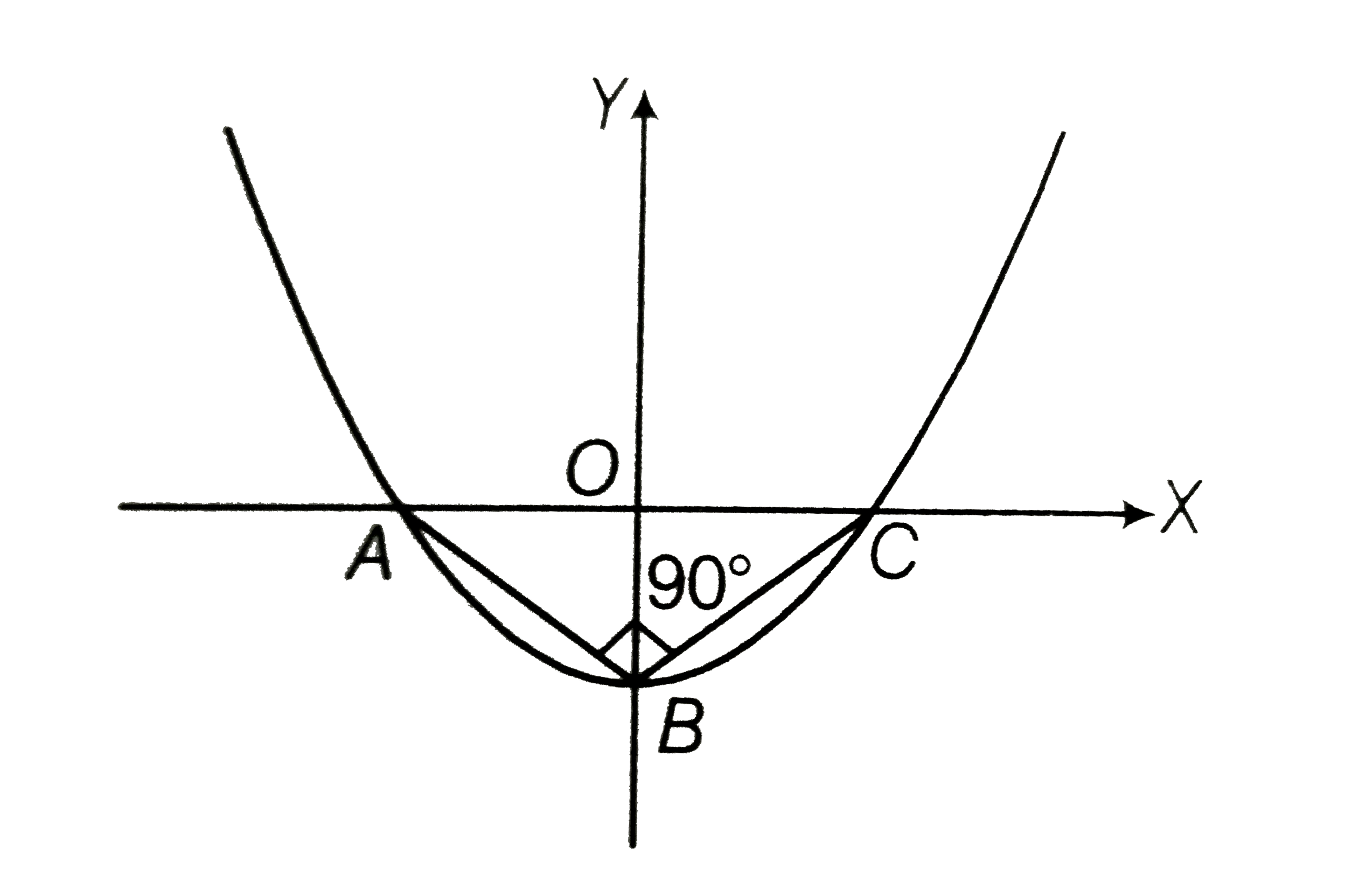
Number of integral value of λ for which λ2 lies between the roots of f(x)=0, is
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.

y=f(x) is given by
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.

Minimum valueof y=f(x) is
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.

Number of integral value of λ for which λ2 lies between the roots of f(x)=0, is
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.

y=f(x) is given by
View Solution
