Solve the equation
2|x+1|−2x=|2x−1|+1 Solution in Kannada
Video Solution
Text Solution
Find the critical points:brgt 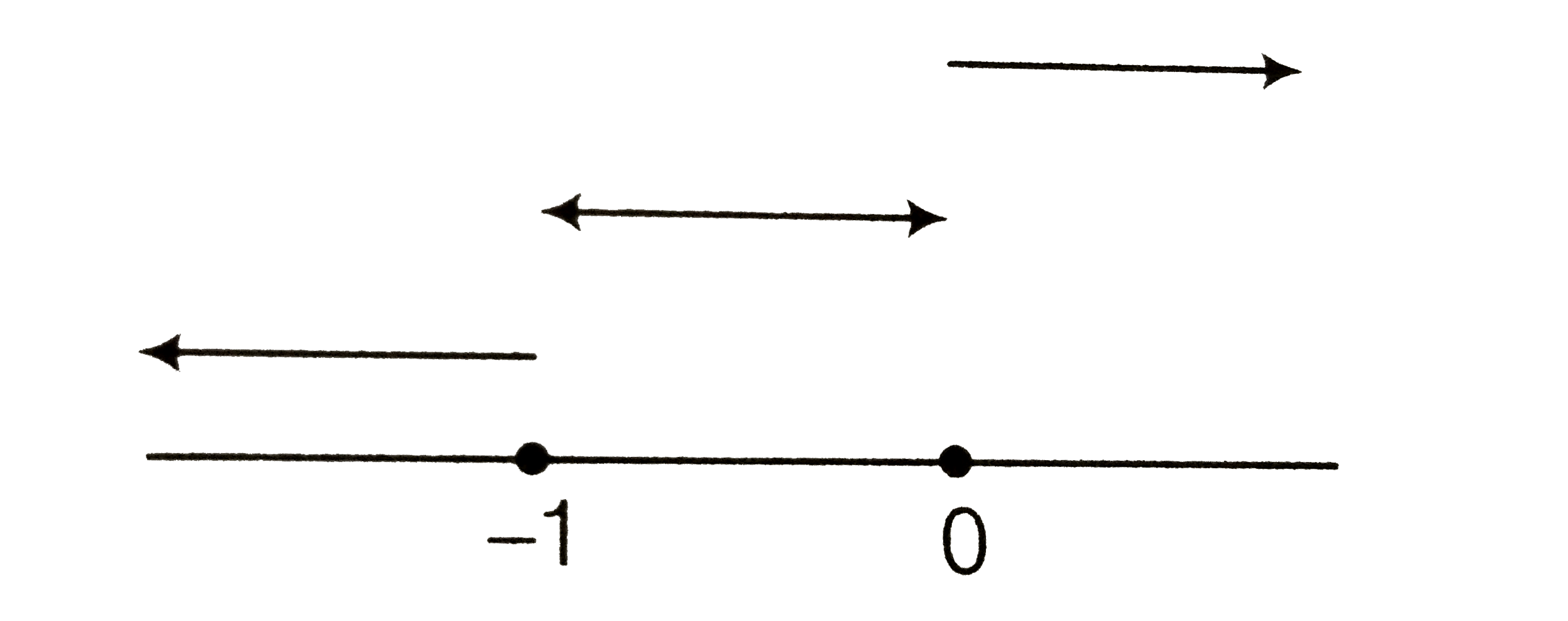
x+1=0,2x−1=0
∴x=−1,x=0
Now consider the following cases,
x<−1
2−(x+1)−2x=−(2x−1)+1
⇒2−(x+1)=2
∴−(x+1)=1
∴x=−2..i
−1≤x<0 ltbr 2x+1−2x=−(2x−1)+1
⇒2x+1=2
∴x+1=1
∴x=0
x≠[∵−1≤x<0]
x≥0
2x+1−2x=2x−1+1
⇒2x+1=2.2x
⇒2x+1=2x+1
which is true for x≥0..............ii
Now, combining all cases we have the final solution as
xε[0,∞)∪{−2}
|
Similar Questions
समीकरण x+1x+xx+1=52 को हल कीजिये।
View Solutionसमीकरण x+1x+xx+1=52 को हल कीजिये।
View SolutionSolve the equation x(x+2)(x2−1)=−1.
View SolutionSolve the equation x(x+2)(x2−1)=−1.
View Solutionद्विघात समीकरण हल कीजिए : x+1x−1+2+xx−2=2x+13x+1.
View SolutionSolve the equation ∣∣∣xx−1∣∣∣+|x|=x2|x−1|
View SolutionSolve the following equations : 2(xx+1)2−5(xx+1)+2=0 x≠−1
View SolutionSolve the equation x(x+2)(x2−1)=−1.
View Solution
